Branching by Edmonds: Difference between revisions
| (71 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
'''Algorithmic problem:''' [[Maximum branching]] | '''Algorithmic problem:''' [[Maximum branching]] | ||
''' | '''Type of algorithm:''' recursion | ||
''' | '''Invariant:''' The output of a recursive call is a maximum branching of the weighted graph that was the input for this recursive call. | ||
''' | '''Definition:''' | ||
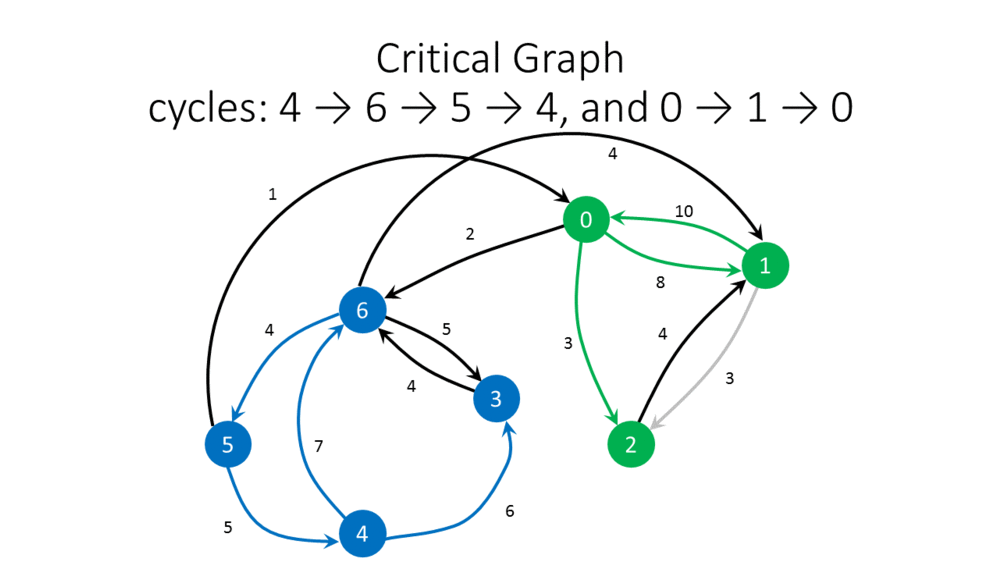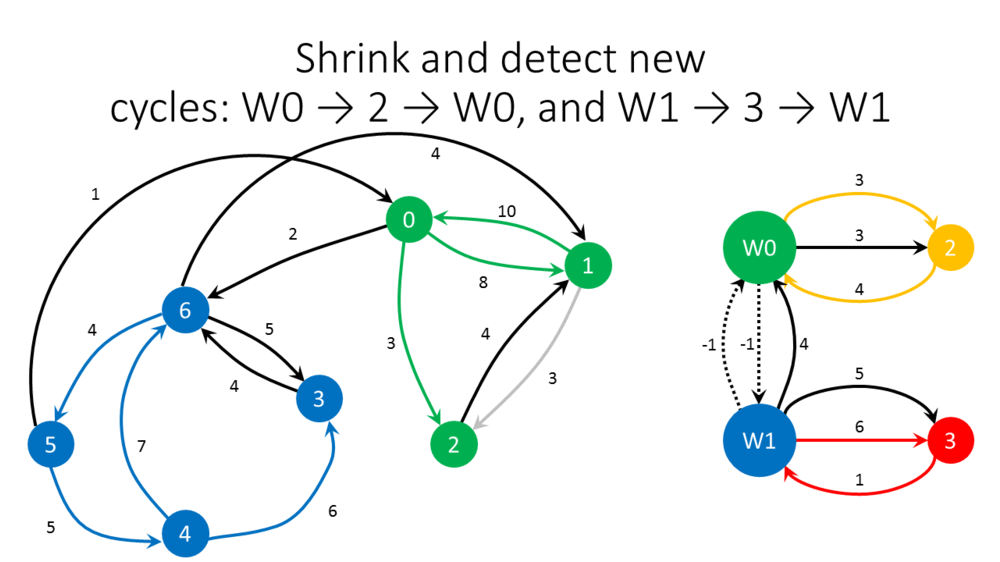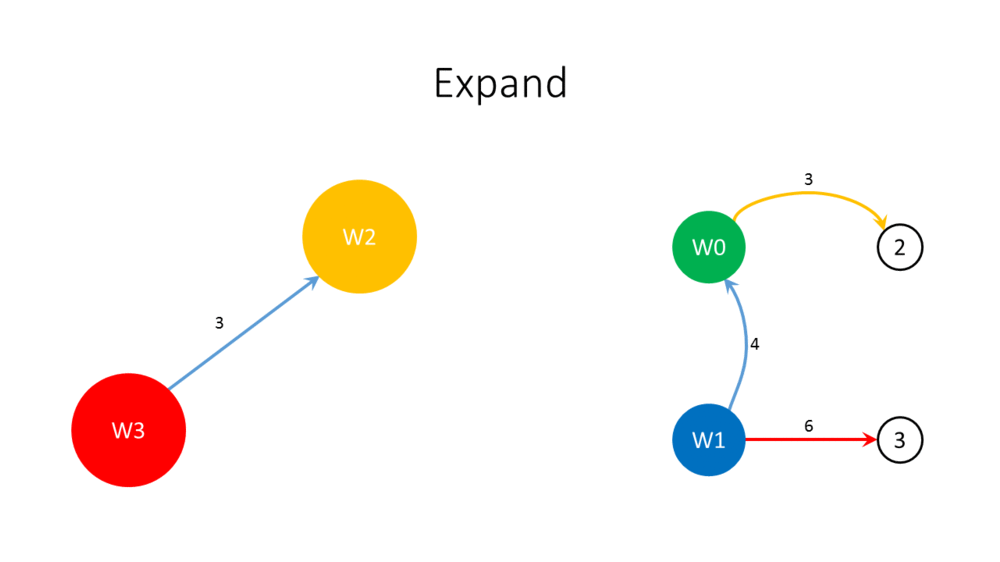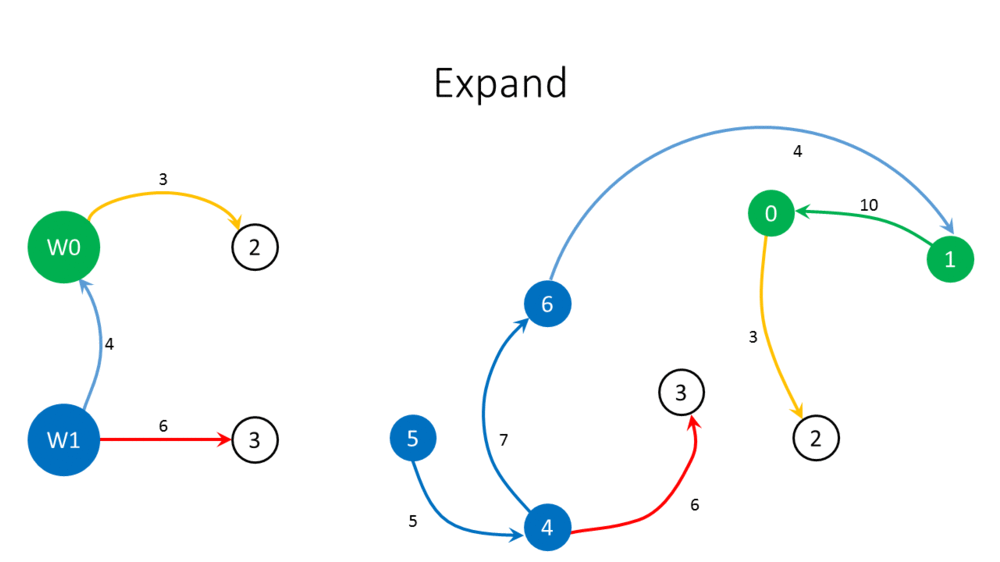
# An arc <math>(v,w)\in A</math> is '''critical''' for <math>w\in V</math> if its weight is not smaller than the weight of any other incoming arc of <math>w</math>. | |||
# A '''critical subgraph''' <math>G'=(V,A')</math> of <math>G</math> contains exactly one incoming arc <math>(v,w)\in A</math> for each node <math>w\in V</math> of positive indegree, where <math>(v,w)</math> is critical. | |||
In each recursive call, first a critical subgraph <math>G'</math> of <math>G</math> is computed. | |||
== | == Recursion anchor == | ||
'''Abstract view:''' Terminate if <math>G'</math> is cycle-free. | '''Abstract view:''' Terminate if <math>G'</math> is cycle-free. | ||
| Line 22: | Line 22: | ||
By definition, a critical graph contains one incoming arc for each node that does have incoming arcs. Therefore, for each arc <math>a</math> of <math>B</math>, there is an arc <math>a'</math> in <math>G'</math> pointing to the same node. Due to the choice of arcs for <math>G'</math>, it is <math>w(a)\leq w(a')</math>. | By definition, a critical graph contains one incoming arc for each node that does have incoming arcs. Therefore, for each arc <math>a</math> of <math>B</math>, there is an arc <math>a'</math> in <math>G'</math> pointing to the same node. Due to the choice of arcs for <math>G'</math>, it is <math>w(a)\leq w(a')</math>. | ||
== | == Recursive step == | ||
[[File:Edmonds max branching ani 10000.gif|thumb|350px|''animated gif:'' Branching by Edmonds]] | |||
'''Abstract view:''' | '''Abstract view:''' | ||
# Identify some cycle <math> | # Identify some cycle <math>C</math> in <math>G'</math>. | ||
# Let <math>W</math> denote the minimum weight of all arcs on <math> | # Let <math>W</math> denote the minimum weight of all arcs on <math>C</math>. | ||
# For every arc <math>(v,w)\in A</math> pointing from some node <math>v</math> outside <math> | # For every arc <math>(v,w)\in A</math> pointing from some node <math>v</math> outside <math>C</math> to some node <math>w</math> on <math>C</math>: | ||
# Shrink <math> | ##Decrease the weight of <math>(v,w)</math> by <math>w(v',w)-W\geq 0</math>, where <math>(v',w)</math> is the incoming arc of <math>w</math> on <math>C</math>. | ||
## If the new weight of <math>(v,w)</math> is not positive, remove <math>(v,w)</math> from <math>G</math>. | |||
# Shrink <math>C</math> into one new super-node, where every arc pointing to (resp., from) some node on <math>C</math> now points to (from) that super-node. | |||
# Call the algorithm recursively for the modified weighted graph after shrinking, giving branching <math>B</math>. | # Call the algorithm recursively for the modified weighted graph after shrinking, giving branching <math>B</math>. | ||
# Unshrink the graph. | # Unshrink the graph. | ||
# Add all arcs of <math> | # Add all arcs of <math>C</math> to <math>B</math> giving <math>B'</math>. | ||
# If <math>B</math> contains an arc <math>(v,w)</math> such that <math>v</math> is outside <math> | # If <math>B'</math> contains an arc <math>(v,w)</math> such that <math>v</math> is outside <math>C</math> and <math>w</math> is on <math>C</math>: remove the incoming arc of <math>w</math> on <math>C</math> from <math>B</math>; otherwise, remove one arc with weight <math>W</math> on <math>C</math>. Let <math>B''</math> be the result in both cases. | ||
# Return <math>B</math>. | # Return <math>B''</math>. | ||
'''Proof:''' | '''Proof:''' | ||
Obviously, <math>B''</math> is a branching, so we have to prove that it has maximum weight | Obviously, <math>B''</math> is a branching, so we have to prove that it has maximum weight among all branchings in <math>G</math>. Let <math>B_{\mathrm{opt}}</math> be a maximum branching in <math>G</math> such that, among all maximum branchings in <math>G</math>, <math>B_{\mathrm{opt}}</math> shares as many arcs as possible with <math>B''</math>. | ||
Let <math>C'</math> be a cycle of <math>G'</math> (the case <math>C'=C</math> not excluded). First we show that <math>B_{\mathrm{opt}}</math> contains all arcs of <math>C'</math> except one. So, suppose for a contradiction that <math>B_{\mathrm{opt}}</math> does not contain some of the arcs of <math>C'</math>, say, <math>(v_1,w_1),\ldots,(v_k,w_k)</math> with <math>k>1</math>. | |||
Replacing the incoming arc of any <math>w_i</math> by <math>(v_i,w_i)</math> in <math>B_{\mathrm{opt}}</math> and doing nothing else, would not decrease the total weight. Since <math>B_{\mathrm{opt}}</math> is as close as possible to <math>B''</math>, such a replacement cannot result in a branching anymore. Since the indegrees do not change by that replacement, this means that adding <math>(v_i,w_i)</math> to <math>B_{\mathrm{opt}}</math> would close a cycle. In other words, there is a path <math>p_i</math> in <math>B_{\mathrm{opt}}</math> from <math>w_i</math> to <math>v_i</math>. Each path <math>p_i</math> must enter <math>C'</math> at one of the nodes <math>w_j</math> (actually at the nearest <math>w_j</math> looking backwards from <math>v_i</math> on <math>C'</math>) because, otherwise, the node where <math>p_i</math> enters <math>C'</math> had two incoming arcs in <math>B_{\mathrm{opt}}</math>: the incoming arc on <math>C'</math> and the arc over which <math>p_i</math> enters <math>C'</math>. However, this would imply that there is a cycle in the union of all paths <math>p_i</math>. This union is a subset of <math>B_{\mathrm{opt}}</math>, which yields the desired contradiction. | |||
Now we know that <math>B_{\mathrm{opt}}</math> contains all arcs except one on all cycles of <math>G'</math>. Note that, for any node not on a cycle, the incoming branching arc may be freely chosen (except for arcs which would close a cycle) without any effect on the rest. So, since <math>B_{\mathrm{opt}}</math> is as close as possible to <math>B''</math>,<math>B_{\mathrm{opt}}</math> and <math>B''</math> agree on all of these choices. Further note that all cycles of <math>G'</math> are node-disjoint. In summary, we may compare <math>B_{\mathrm{opt}}</math> and <math>B''</math> on each cycle of <math>G'</math> separately. | |||
For <math>C</math>, complete agreement between <math>B_{\mathrm{opt}}</math> and <math>B''</math> follows from the observation that the choice of incoming arcs for all nodes on <math>C</math> is optimal in <math>B''</math> due to the specific modification of the arc weights. And for all other cycles of <math>G'</math>, complete agreement follows from the induction hypothesis. In both cases, we again used the specific choice of <math>B_{\mathrm{opt}}</math> to be as close to <math>B''</math> as possible. | |||
== Complexity == | == Complexity == | ||
| Line 46: | Line 54: | ||
'''Proof:''' | '''Proof:''' | ||
Using [[DFS]] for cycle detection, each recursive step requires <math>\mathcal{O}(n+m)</math>. In each shrink operation, the number of nodes decreases, so the recursion depth is <math>\mathcal{O}(n)</math>. | Using [[Depth-first search|DFS]] for cycle detection, each recursive step requires <math>\mathcal{O}(n+m)</math>. In each shrink operation, the number of nodes decreases, so the recursion depth is <math>\mathcal{O}(n)</math>. | ||
'''Remark:''' | |||
More sophisticated implementations of this algorithm yield better asymptotic complexities. | |||
== Remarks == | == Remarks == | ||
# The unshrink operation requires that the shrink operation performs some bookkeeping: For the super-node, a cyclically ordered sequence of all nodes and arcs on <math> | # The unshrink operation requires that the shrink operation performs some bookkeeping: For the super-node, a cyclically ordered sequence of all nodes and arcs on <math>C</math> (or an equivalent bulk of information) must be attached to a super-node. | ||
# Several cycles may be discovered simultaneously by one run of [[DFS]]. Note that all cycles in a critical graph are node-disjoint, because no node has more than one incoming arc. Therefore, several cycles may be handled | # Several cycles may be discovered simultaneously by one run of [[Depth-first search|DFS]]. Note that all cycles in a critical graph are node-disjoint, because no node has more than one incoming arc. Therefore, several cycles may be handled in the same recursive call, without any interference. | ||
Latest revision as of 07:59, 8 November 2015
Abstract view
Algorithmic problem: Maximum branching
Type of algorithm: recursion
Invariant: The output of a recursive call is a maximum branching of the weighted graph that was the input for this recursive call.
Definition:
- An arc [math]\displaystyle{ (v,w)\in A }[/math] is critical for [math]\displaystyle{ w\in V }[/math] if its weight is not smaller than the weight of any other incoming arc of [math]\displaystyle{ w }[/math].
- A critical subgraph [math]\displaystyle{ G'=(V,A') }[/math] of [math]\displaystyle{ G }[/math] contains exactly one incoming arc [math]\displaystyle{ (v,w)\in A }[/math] for each node [math]\displaystyle{ w\in V }[/math] of positive indegree, where [math]\displaystyle{ (v,w) }[/math] is critical.
In each recursive call, first a critical subgraph [math]\displaystyle{ G' }[/math] of [math]\displaystyle{ G }[/math] is computed.
Recursion anchor
Abstract view: Terminate if [math]\displaystyle{ G' }[/math] is cycle-free.
Proof: If [math]\displaystyle{ G' }[/math] is cycle-free, it is a branching. Consider some other branching [math]\displaystyle{ B }[/math]. We have to show that [math]\displaystyle{ B }[/math] does not have more total weight than [math]\displaystyle{ G' }[/math].
By definition, a critical graph contains one incoming arc for each node that does have incoming arcs. Therefore, for each arc [math]\displaystyle{ a }[/math] of [math]\displaystyle{ B }[/math], there is an arc [math]\displaystyle{ a' }[/math] in [math]\displaystyle{ G' }[/math] pointing to the same node. Due to the choice of arcs for [math]\displaystyle{ G' }[/math], it is [math]\displaystyle{ w(a)\leq w(a') }[/math].
Recursive step
Abstract view:
- Identify some cycle [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G' }[/math].
- Let [math]\displaystyle{ W }[/math] denote the minimum weight of all arcs on [math]\displaystyle{ C }[/math].
- For every arc [math]\displaystyle{ (v,w)\in A }[/math] pointing from some node [math]\displaystyle{ v }[/math] outside [math]\displaystyle{ C }[/math] to some node [math]\displaystyle{ w }[/math] on [math]\displaystyle{ C }[/math]:
- Decrease the weight of [math]\displaystyle{ (v,w) }[/math] by [math]\displaystyle{ w(v',w)-W\geq 0 }[/math], where [math]\displaystyle{ (v',w) }[/math] is the incoming arc of [math]\displaystyle{ w }[/math] on [math]\displaystyle{ C }[/math].
- If the new weight of [math]\displaystyle{ (v,w) }[/math] is not positive, remove [math]\displaystyle{ (v,w) }[/math] from [math]\displaystyle{ G }[/math].
- Shrink [math]\displaystyle{ C }[/math] into one new super-node, where every arc pointing to (resp., from) some node on [math]\displaystyle{ C }[/math] now points to (from) that super-node.
- Call the algorithm recursively for the modified weighted graph after shrinking, giving branching [math]\displaystyle{ B }[/math].
- Unshrink the graph.
- Add all arcs of [math]\displaystyle{ C }[/math] to [math]\displaystyle{ B }[/math] giving [math]\displaystyle{ B' }[/math].
- If [math]\displaystyle{ B' }[/math] contains an arc [math]\displaystyle{ (v,w) }[/math] such that [math]\displaystyle{ v }[/math] is outside [math]\displaystyle{ C }[/math] and [math]\displaystyle{ w }[/math] is on [math]\displaystyle{ C }[/math]: remove the incoming arc of [math]\displaystyle{ w }[/math] on [math]\displaystyle{ C }[/math] from [math]\displaystyle{ B }[/math]; otherwise, remove one arc with weight [math]\displaystyle{ W }[/math] on [math]\displaystyle{ C }[/math]. Let [math]\displaystyle{ B'' }[/math] be the result in both cases.
- Return [math]\displaystyle{ B'' }[/math].
Proof: Obviously, [math]\displaystyle{ B'' }[/math] is a branching, so we have to prove that it has maximum weight among all branchings in [math]\displaystyle{ G }[/math]. Let [math]\displaystyle{ B_{\mathrm{opt}} }[/math] be a maximum branching in [math]\displaystyle{ G }[/math] such that, among all maximum branchings in [math]\displaystyle{ G }[/math], [math]\displaystyle{ B_{\mathrm{opt}} }[/math] shares as many arcs as possible with [math]\displaystyle{ B'' }[/math].
Let [math]\displaystyle{ C' }[/math] be a cycle of [math]\displaystyle{ G' }[/math] (the case [math]\displaystyle{ C'=C }[/math] not excluded). First we show that [math]\displaystyle{ B_{\mathrm{opt}} }[/math] contains all arcs of [math]\displaystyle{ C' }[/math] except one. So, suppose for a contradiction that [math]\displaystyle{ B_{\mathrm{opt}} }[/math] does not contain some of the arcs of [math]\displaystyle{ C' }[/math], say, [math]\displaystyle{ (v_1,w_1),\ldots,(v_k,w_k) }[/math] with [math]\displaystyle{ k\gt 1 }[/math].
Replacing the incoming arc of any [math]\displaystyle{ w_i }[/math] by [math]\displaystyle{ (v_i,w_i) }[/math] in [math]\displaystyle{ B_{\mathrm{opt}} }[/math] and doing nothing else, would not decrease the total weight. Since [math]\displaystyle{ B_{\mathrm{opt}} }[/math] is as close as possible to [math]\displaystyle{ B'' }[/math], such a replacement cannot result in a branching anymore. Since the indegrees do not change by that replacement, this means that adding [math]\displaystyle{ (v_i,w_i) }[/math] to [math]\displaystyle{ B_{\mathrm{opt}} }[/math] would close a cycle. In other words, there is a path [math]\displaystyle{ p_i }[/math] in [math]\displaystyle{ B_{\mathrm{opt}} }[/math] from [math]\displaystyle{ w_i }[/math] to [math]\displaystyle{ v_i }[/math]. Each path [math]\displaystyle{ p_i }[/math] must enter [math]\displaystyle{ C' }[/math] at one of the nodes [math]\displaystyle{ w_j }[/math] (actually at the nearest [math]\displaystyle{ w_j }[/math] looking backwards from [math]\displaystyle{ v_i }[/math] on [math]\displaystyle{ C' }[/math]) because, otherwise, the node where [math]\displaystyle{ p_i }[/math] enters [math]\displaystyle{ C' }[/math] had two incoming arcs in [math]\displaystyle{ B_{\mathrm{opt}} }[/math]: the incoming arc on [math]\displaystyle{ C' }[/math] and the arc over which [math]\displaystyle{ p_i }[/math] enters [math]\displaystyle{ C' }[/math]. However, this would imply that there is a cycle in the union of all paths [math]\displaystyle{ p_i }[/math]. This union is a subset of [math]\displaystyle{ B_{\mathrm{opt}} }[/math], which yields the desired contradiction.
Now we know that [math]\displaystyle{ B_{\mathrm{opt}} }[/math] contains all arcs except one on all cycles of [math]\displaystyle{ G' }[/math]. Note that, for any node not on a cycle, the incoming branching arc may be freely chosen (except for arcs which would close a cycle) without any effect on the rest. So, since [math]\displaystyle{ B_{\mathrm{opt}} }[/math] is as close as possible to [math]\displaystyle{ B'' }[/math],[math]\displaystyle{ B_{\mathrm{opt}} }[/math] and [math]\displaystyle{ B'' }[/math] agree on all of these choices. Further note that all cycles of [math]\displaystyle{ G' }[/math] are node-disjoint. In summary, we may compare [math]\displaystyle{ B_{\mathrm{opt}} }[/math] and [math]\displaystyle{ B'' }[/math] on each cycle of [math]\displaystyle{ G' }[/math] separately.
For [math]\displaystyle{ C }[/math], complete agreement between [math]\displaystyle{ B_{\mathrm{opt}} }[/math] and [math]\displaystyle{ B'' }[/math] follows from the observation that the choice of incoming arcs for all nodes on [math]\displaystyle{ C }[/math] is optimal in [math]\displaystyle{ B'' }[/math] due to the specific modification of the arc weights. And for all other cycles of [math]\displaystyle{ G' }[/math], complete agreement follows from the induction hypothesis. In both cases, we again used the specific choice of [math]\displaystyle{ B_{\mathrm{opt}} }[/math] to be as close to [math]\displaystyle{ B'' }[/math] as possible.
Complexity
Statement: The asymptotic complexity is in [math]\displaystyle{ \mathcal{O}((n+m)\cdot n) }[/math] in the worst case, where [math]\displaystyle{ n=|V| }[/math] and [math]\displaystyle{ m=|A| }[/math].
Proof: Using DFS for cycle detection, each recursive step requires [math]\displaystyle{ \mathcal{O}(n+m) }[/math]. In each shrink operation, the number of nodes decreases, so the recursion depth is [math]\displaystyle{ \mathcal{O}(n) }[/math].
Remark: More sophisticated implementations of this algorithm yield better asymptotic complexities.
Remarks
- The unshrink operation requires that the shrink operation performs some bookkeeping: For the super-node, a cyclically ordered sequence of all nodes and arcs on [math]\displaystyle{ C }[/math] (or an equivalent bulk of information) must be attached to a super-node.
- Several cycles may be discovered simultaneously by one run of DFS. Note that all cycles in a critical graph are node-disjoint, because no node has more than one incoming arc. Therefore, several cycles may be handled in the same recursive call, without any interference.