Eulerian cycle: Difference between revisions
No edit summary |
|||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
A ''' | # A '''eulerian cycle''' is an [[Basic graph definitions#Cycles|ordinary cycle]] in a directed or undirected graph that contains each edge/arc exactly once. | ||
# A directed or undirected graph is called '''eulerian''' if it admits a eulerian cycle. | |||
'''Remark:''' | |||
It is easy to see (and follows from the [[Classical eulerian cycle algorithm|classical algorithm]]) that a graph <math>G</math> is eulerian if, and only if: | |||
# Undirected case: <math>G</math> is connected, and each node has even degree. | |||
# Directed case: <math>G</math> is strongly connected, and for each node <math>v</math>, the indegree of <math>v</math> equals the outdegree of <math>v</math>. | |||
== Input == | == Input == | ||
| Line 10: | Line 15: | ||
== Output == | == Output == | ||
A | A eulerian cycle as an alternating sequence of nodes and edges/arcs or, alternatively, the (correct) message that the graph is not eulerian. | ||
== Known algorithms == | == Known algorithms == | ||
[[Classical eulerian cycle algorithm]] | [[Classical eulerian cycle algorithm]] | ||
== Historical Approach == | |||
The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and prefigured the idea of topology. The problem was to find a walk through the city that would cross each bridge once and only once. Euler reformulate the problem in abstracts terms and so he replaces each land mass with an abstract node, aka ''vertex'', and each brigde with an abstract connection, aka ''edge''. | |||
[[File:Eulerkonigsberg.png]] | |||
Euler observes that during any walk in the graph, the number of times one enters a vertex equals the number of times one leaves it. It follows that, for every vertex (except start and finish), the number of edges touches that vertex must be even. With this studies, Euler shows that a necessary condition for an ''Eulerian walk'' is that | |||
* the graph is connected and | |||
* have exactly zero or two nodes of odd degree. | |||
Latest revision as of 20:57, 12 November 2014
Definition
- A eulerian cycle is an ordinary cycle in a directed or undirected graph that contains each edge/arc exactly once.
- A directed or undirected graph is called eulerian if it admits a eulerian cycle.
Remark: It is easy to see (and follows from the classical algorithm) that a graph [math]\displaystyle{ G }[/math] is eulerian if, and only if:
- Undirected case: [math]\displaystyle{ G }[/math] is connected, and each node has even degree.
- Directed case: [math]\displaystyle{ G }[/math] is strongly connected, and for each node [math]\displaystyle{ v }[/math], the indegree of [math]\displaystyle{ v }[/math] equals the outdegree of [math]\displaystyle{ v }[/math].
Input
A strongly connected directed or connected undirected graph.
Output
A eulerian cycle as an alternating sequence of nodes and edges/arcs or, alternatively, the (correct) message that the graph is not eulerian.
Known algorithms
Classical eulerian cycle algorithm
Historical Approach
The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and prefigured the idea of topology. The problem was to find a walk through the city that would cross each bridge once and only once. Euler reformulate the problem in abstracts terms and so he replaces each land mass with an abstract node, aka vertex, and each brigde with an abstract connection, aka edge.
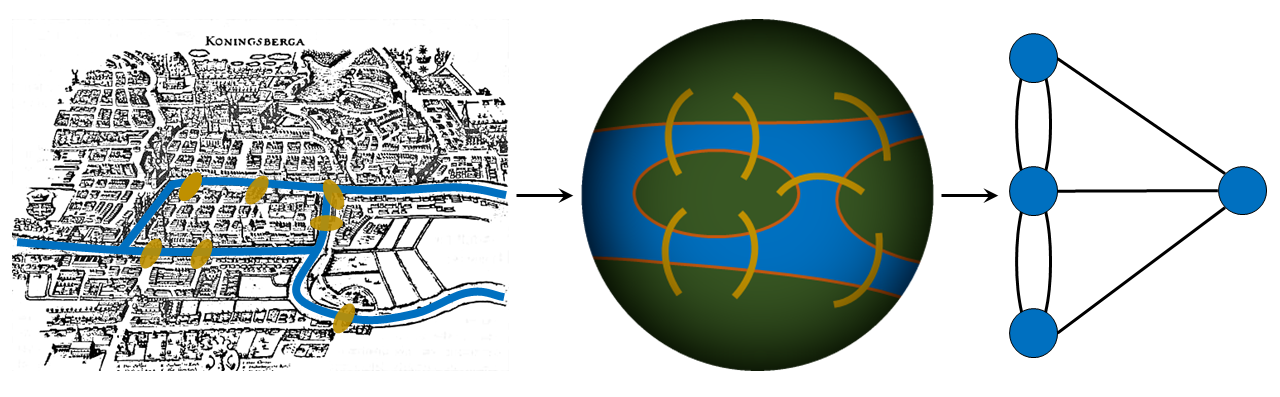
Euler observes that during any walk in the graph, the number of times one enters a vertex equals the number of times one leaves it. It follows that, for every vertex (except start and finish), the number of edges touches that vertex must be even. With this studies, Euler shows that a necessary condition for an Eulerian walk is that
- the graph is connected and
- have exactly zero or two nodes of odd degree.