Quicksort: Difference between revisions
No edit summary |
|||
| (42 intermediate revisions by 5 users not shown) | |||
| Line 6: | Line 6: | ||
<div style="font-size: 1.2em; margin:.5em 0 1em 0; text-align:center">whatever</div> | <div style="font-size: 1.2em; margin:.5em 0 1em 0; text-align:center">whatever</div> | ||
<div style="font-size: 1.2em; margin:.5em 0 .5em 0;text-align:center">[https://openlearnware.tu-darmstadt.de/#!/resource/quick-sort-1945 Openlearnware]</div> | <div style="font-size: 1.2em; margin:.5em 0 .5em 0;text-align:center">[[File:olw_logo1.png|20px]][https://openlearnware.tu-darmstadt.de/#!/resource/quick-sort-1945 Openlearnware]</div> | ||
</div> | </div> | ||
== General information == | |||
'''Algorithmic problem:''' [[Sorting based on pairwise comparison]] | |||
'''Type of algorithm:''' recursion | |||
== Abstract view == | |||
'''Invariant:''' After a recursive call, the input sequence of this recursive call is sorted. | |||
'''Variant:''' In each recursive call, the sequence of the callee is strictly shorter than that of the caller. | |||
'''Break condition:''' The sequence is empty or a [[Sets and sequences#Singleton, pair, triple, quadruple|singleton]]. | |||
'''Remark:''' For a particular recursive call <math>C</math>, we may, for example, choose the height of the recursion subtree with root <math>C</math> as the induction parameter. For conciseness, the induction parameter is omitted in the following. | |||
== Induction basis == | |||
'''Abstract view:''' Nothing to do on an empty sequence or a singleton. | |||
'''Implementation:''' Ditto. | |||
'''Proof:''' Empty sequences and singletons are trivially sorted. | |||
== Induction step == | |||
=== Abstract view: === | |||
# Choose a pivot value <math>p \in [min\{x|x \in S\},\dots,max\{x|x \in S\}]</math> (note that <math>p</math> is not required to be an element of <math>S</math>. | |||
# Partition <math>S</math> into sequences, <math>S_1</math>, <math>S_2</math> and <math>S_3</math>, such that <math>x < p</math> for all <math>x \in S_1</math>, <math>x = p</math> for all <math>x \in S_2</math>, and <math>x > p</math> for all <math>x \in S_3</math>. | |||
# Sort <math>S_1</math> and <math>S_3</math> recursively. | |||
# The concatenation of all three lists, <math>S_1 + S_2 + S_3</math>, is the result of the algorithm. | |||
=== Implementation: === | |||
# Choose <math>p \in [min\{x|x \in S\},\dots,max\{x|x \in S\}]</math> according to some pivoting rule. | |||
# <math>S_1 := S_2 := S_3 := \emptyset</math>. | |||
# For all <math>x \in S</math>, append <math>x</math> to | |||
## <math>S_1</math> if <math>x < p</math>, | |||
## <math>S_2</math> if <math>x = p</math>, | |||
## <math>S_3</math> if <math>x > p</math>. | |||
# Call Quicksort on <math>S_1</math> giving <math>S_1'</math> | |||
# Call Quicksort on <math>S_3</math> giving <math>S_3'</math> | |||
# Return <math>S_1' + S_2' + S_3'</math>. | |||
=== Correctness: === | |||
By induction hypothesis, <math>S_1'</math> and <math>S_3'</math> are sorted permutations of <math>S_1</math> and <math>S_3</math>, respectively. In particular <math>S_1' + S_2 + S_3'</math> is a permutation of <math>S</math>. To see that this permutation is sorted, let <math>x</math> and <math>y</math> be two members of <math>S</math> such that <math>y</math> immediately succeeds <math>x</math> in the resulting sequence <math>S_1' + S_2 + S_3'</math>. We have to show <math>x \leq y</math>. | |||
# If <math>x,y \in S_1'</math> or <math>x,y \in S_3'</math>, <math>x \leq y</math> resultes from the induction hypothesis. | |||
# On the other hand, if <math>x,y \in S_2</math>. It is <math>x = y = p</math>, which trivially implies <math>x \leq y</math>. | |||
# Finally, for the following cases, <math>x \leq y</math> is implied by the specific way of partitioning <math>S</math> into <math>S_1'</math>, <math>S_2</math> and <math>S_3'</math>: | |||
## <math>x \in S_1'</math> and <math>y \in S_2</math> | |||
## <math>x \in S_2</math> and <math>y \in S_3'</math> | |||
## <math>x \in S_1'</math> and <math>y \in S_3'</math> | |||
Obviously, this case distinction covers all potential cases, so the claim is proved. | |||
== Complexity == | |||
=== Statement: === | |||
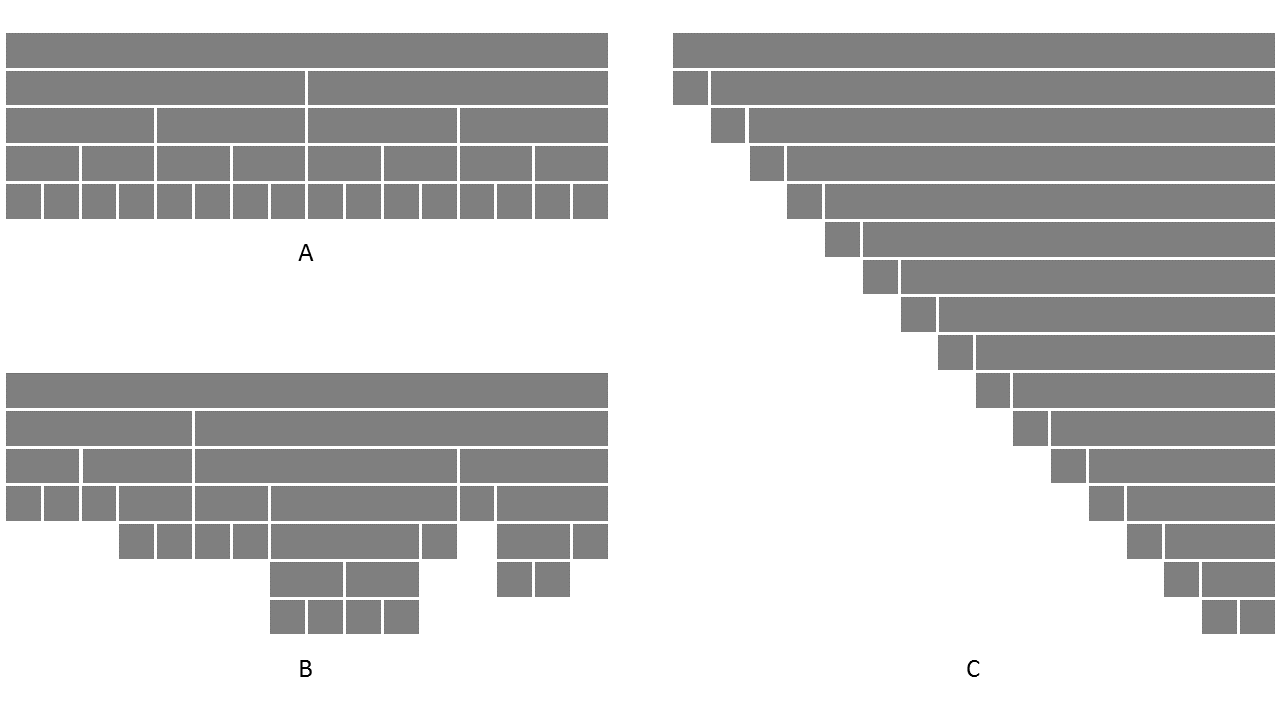
[[File:Quicksortrecursion.png|350px|thumb|right|recursion depth of quick sort : [A] best case, [B] avg. case, [C] worst case]] | |||
In the worst case, the complexity is <math>\Theta(T\cdot n^2)</math>, where <math>T</math> is the complexity of the comparison. | |||
If the pivoting rule ensures for some <math>\alpha < 1</math> that the lengths of <math>S_1</math> and <math>S_3</math> are at most <math>\alpha</math> times the size of <math>S</math>, then it is even <math>\Theta(T\cdot n \log n)</math> in the worst case. | |||
If each pivot value is chosen uniformly randomly from members of the respective sequence and if all selections of pivot values are stochastically independent, the average-case complexity is <math>\Theta(T\cdot n \log n)</math>. | |||
=== Proof: === | |||
First note that the complexity for a single recursive call on <math>S</math> (excluding the complexity for the recursive descents on <math>S_1</math> and <math>S_3</math>) is in <math>\Theta(T\cdot|S|)</math>. On each recursive level, all calls are on distinct subsets of <math>S</math>. Therefore, the number of recursive calls with non-empty sequences on one recursive level is in <math>\Theta(n)</math>. The number of calls with empty sequences on one level is at most twice the total number of calls with non-empty sequences on the previous level. Hence, the number of calls with empty sequences on one recursive level is in <math>O(n)</math> as well. In summary, the total complexity on a recursive level is <math>O(T\cdot n)</math>. So, for the total complexity, it remains to estimate the number of recursive levels. | |||
Now consider the first statement. The recursion variant implies that the deepest recursive level is <math>O(n)</math>. On the other hand, <math>\Omega(n)</math> in the very worst case is obvious. This gives the claimed <math>\Theta(T\cdot n^2)</math> in the worst case. | |||
Next assume there is a fixed <math>\alpha < 1</math> such that <math>|S_1| \leq \alpha \cdot|S|</math> and <math>|S_3| \leq \alpha \cdot|S|</math> is guaranteed in each recursive call. Then the length of any sequence on recursive level <math>\#i</math> is at most <math>\alpha ^ i \cdot |S|</math>. Therefore, the maximal recursive depth is <math>\lceil \log_{a^{-1}}(n)\rceil</math>. Since <math>\alpha^{-1} > 1</math>, the total complexity is in <math>O(T\cdot n \log n)</math> in the worst case. | |||
For the last statement, the average-case analysis, first note that the number of comparisons alone has the same asymptotic complexity as the algorithm as a whole. Next note that any <math>x,y \in S</math> are compared at most once throughout the entire algorithm if, and only if, <math>x</math> or <math>y</math> is chosen as the pivot value for a subsequence to which both elements belong. For <math>x,y \in S</math>, let <math>Pr(x,y)</math> denote the probability that <math>x</math> and <math>y</math> are indeed compared. Since comparison events are distinct and <math>Pr(x,y )\in \{0,1\}</math> for all <math>x,y \in S</math>, the expected number of comparisons is | |||
<math>\sum_{x,y \in S, x \neq y} Pr(x,y)</math> | |||
Let <math>n := |S|</math>, and for <math>i,j \in \{1,\dots,n\}</math>, let <math>Pr(i,j)</math> denote the probability that the <math>i</math>-th and the <math>j</math>-th elemet of the eventual sorted sequence are compared throughout the algorithm. Using this notation, we may rewrite the above summation as follows: | |||
<math>\sum_{x,y \in S, x \neq y} Pr(x,y) = \sum_{i=1}^{n-1} \sum_{j = i+1}^{n} Pr(i,j)</math>. | |||
For <math>i,j \in \{1,\dots,n\}</math>, <math>i < j</math>, let <math> S_{ij}</math> denote the subsequence of the eventual sorted sequence that starts with <math>i</math> and ends with <math>j</math>. The elements <math>\#i</math> and <math>\#j</math> are compared if, and only if, <math>\#i</math> or <math>\#j</math> is the very first element of <math>S_{ij}</math> to be chosen as a pivot. The probability of this event is <math>\frac{2}{|S_{ij}|} = \frac{2}{j - i + 1}</math>, so we obtain | |||
<math>\sum_{i=1}^{n-1} \sum_{j = i+1}^{n} \frac{2}{j-i+1}</math>. | |||
Substituting <math>k := j-i</math>, this gives | |||
<math>\sum_{i=1}^{n-1} \sum_{j = i+1}^{n} \frac{2}{j-i+1} = \sum_{i=1}^{n-1} \sum_{k=1}^{n} \frac{2}{k+1} \leq 2(n - 1)</math>. | |||
<math>\sum_{k=1}^n \frac{1}{k+1} \leq 2(n-1)</math>. | |||
<math>\sum_{k+1}^n \frac{1}{k}</math>. | |||
The [http://en.wikipedia.org/wiki/Harmonic_series_(mathematics)#Rate_of_divergence asymptotic behavior] of the [http://en.wikipedia.org/wiki/Harmonic_series_(mathematics) harmonic series] is <math>\Theta(\log n)</math>, so the last expression is <math>\Theta(T\cdot n \log n)</math>. | |||
== Further information == | |||
If <math>S</math> is an array, <math>S</math> cannot be decomposed into subsequences. We would liko to avoid the need for additional arrays and copy operations. Instead, the array should be sorted in-place, that is, by swap operations on pairs of elements. The auxiliary procedure, [[Pivot partitioning by scanning]], is designed exactly for that: it permutes the array such that each of <math>S_1</math> and <math>S_2</math> is a subarray. Then each recursive call of Quicksort operates on a subarray of the input array, which is specified by two index pointers. | |||
Latest revision as of 13:36, 3 March 2017
General information
Algorithmic problem: Sorting based on pairwise comparison
Type of algorithm: recursion
Abstract view
Invariant: After a recursive call, the input sequence of this recursive call is sorted.
Variant: In each recursive call, the sequence of the callee is strictly shorter than that of the caller.
Break condition: The sequence is empty or a singleton.
Remark: For a particular recursive call [math]\displaystyle{ C }[/math], we may, for example, choose the height of the recursion subtree with root [math]\displaystyle{ C }[/math] as the induction parameter. For conciseness, the induction parameter is omitted in the following.
Induction basis
Abstract view: Nothing to do on an empty sequence or a singleton.
Implementation: Ditto.
Proof: Empty sequences and singletons are trivially sorted.
Induction step
Abstract view:
- Choose a pivot value [math]\displaystyle{ p \in [min\{x|x \in S\},\dots,max\{x|x \in S\}] }[/math] (note that [math]\displaystyle{ p }[/math] is not required to be an element of [math]\displaystyle{ S }[/math].
- Partition [math]\displaystyle{ S }[/math] into sequences, [math]\displaystyle{ S_1 }[/math], [math]\displaystyle{ S_2 }[/math] and [math]\displaystyle{ S_3 }[/math], such that [math]\displaystyle{ x \lt p }[/math] for all [math]\displaystyle{ x \in S_1 }[/math], [math]\displaystyle{ x = p }[/math] for all [math]\displaystyle{ x \in S_2 }[/math], and [math]\displaystyle{ x \gt p }[/math] for all [math]\displaystyle{ x \in S_3 }[/math].
- Sort [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_3 }[/math] recursively.
- The concatenation of all three lists, [math]\displaystyle{ S_1 + S_2 + S_3 }[/math], is the result of the algorithm.
Implementation:
- Choose [math]\displaystyle{ p \in [min\{x|x \in S\},\dots,max\{x|x \in S\}] }[/math] according to some pivoting rule.
- [math]\displaystyle{ S_1 := S_2 := S_3 := \emptyset }[/math].
- For all [math]\displaystyle{ x \in S }[/math], append [math]\displaystyle{ x }[/math] to
- [math]\displaystyle{ S_1 }[/math] if [math]\displaystyle{ x \lt p }[/math],
- [math]\displaystyle{ S_2 }[/math] if [math]\displaystyle{ x = p }[/math],
- [math]\displaystyle{ S_3 }[/math] if [math]\displaystyle{ x \gt p }[/math].
- Call Quicksort on [math]\displaystyle{ S_1 }[/math] giving [math]\displaystyle{ S_1' }[/math]
- Call Quicksort on [math]\displaystyle{ S_3 }[/math] giving [math]\displaystyle{ S_3' }[/math]
- Return [math]\displaystyle{ S_1' + S_2' + S_3' }[/math].
Correctness:
By induction hypothesis, [math]\displaystyle{ S_1' }[/math] and [math]\displaystyle{ S_3' }[/math] are sorted permutations of [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_3 }[/math], respectively. In particular [math]\displaystyle{ S_1' + S_2 + S_3' }[/math] is a permutation of [math]\displaystyle{ S }[/math]. To see that this permutation is sorted, let [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] be two members of [math]\displaystyle{ S }[/math] such that [math]\displaystyle{ y }[/math] immediately succeeds [math]\displaystyle{ x }[/math] in the resulting sequence [math]\displaystyle{ S_1' + S_2 + S_3' }[/math]. We have to show [math]\displaystyle{ x \leq y }[/math].
- If [math]\displaystyle{ x,y \in S_1' }[/math] or [math]\displaystyle{ x,y \in S_3' }[/math], [math]\displaystyle{ x \leq y }[/math] resultes from the induction hypothesis.
- On the other hand, if [math]\displaystyle{ x,y \in S_2 }[/math]. It is [math]\displaystyle{ x = y = p }[/math], which trivially implies [math]\displaystyle{ x \leq y }[/math].
- Finally, for the following cases, [math]\displaystyle{ x \leq y }[/math] is implied by the specific way of partitioning [math]\displaystyle{ S }[/math] into [math]\displaystyle{ S_1' }[/math], [math]\displaystyle{ S_2 }[/math] and [math]\displaystyle{ S_3' }[/math]:
- [math]\displaystyle{ x \in S_1' }[/math] and [math]\displaystyle{ y \in S_2 }[/math]
- [math]\displaystyle{ x \in S_2 }[/math] and [math]\displaystyle{ y \in S_3' }[/math]
- [math]\displaystyle{ x \in S_1' }[/math] and [math]\displaystyle{ y \in S_3' }[/math]
Obviously, this case distinction covers all potential cases, so the claim is proved.
Complexity
Statement:
In the worst case, the complexity is [math]\displaystyle{ \Theta(T\cdot n^2) }[/math], where [math]\displaystyle{ T }[/math] is the complexity of the comparison.
If the pivoting rule ensures for some [math]\displaystyle{ \alpha \lt 1 }[/math] that the lengths of [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_3 }[/math] are at most [math]\displaystyle{ \alpha }[/math] times the size of [math]\displaystyle{ S }[/math], then it is even [math]\displaystyle{ \Theta(T\cdot n \log n) }[/math] in the worst case.
If each pivot value is chosen uniformly randomly from members of the respective sequence and if all selections of pivot values are stochastically independent, the average-case complexity is [math]\displaystyle{ \Theta(T\cdot n \log n) }[/math].
Proof:
First note that the complexity for a single recursive call on [math]\displaystyle{ S }[/math] (excluding the complexity for the recursive descents on [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_3 }[/math]) is in [math]\displaystyle{ \Theta(T\cdot|S|) }[/math]. On each recursive level, all calls are on distinct subsets of [math]\displaystyle{ S }[/math]. Therefore, the number of recursive calls with non-empty sequences on one recursive level is in [math]\displaystyle{ \Theta(n) }[/math]. The number of calls with empty sequences on one level is at most twice the total number of calls with non-empty sequences on the previous level. Hence, the number of calls with empty sequences on one recursive level is in [math]\displaystyle{ O(n) }[/math] as well. In summary, the total complexity on a recursive level is [math]\displaystyle{ O(T\cdot n) }[/math]. So, for the total complexity, it remains to estimate the number of recursive levels.
Now consider the first statement. The recursion variant implies that the deepest recursive level is [math]\displaystyle{ O(n) }[/math]. On the other hand, [math]\displaystyle{ \Omega(n) }[/math] in the very worst case is obvious. This gives the claimed [math]\displaystyle{ \Theta(T\cdot n^2) }[/math] in the worst case.
Next assume there is a fixed [math]\displaystyle{ \alpha \lt 1 }[/math] such that [math]\displaystyle{ |S_1| \leq \alpha \cdot|S| }[/math] and [math]\displaystyle{ |S_3| \leq \alpha \cdot|S| }[/math] is guaranteed in each recursive call. Then the length of any sequence on recursive level [math]\displaystyle{ \#i }[/math] is at most [math]\displaystyle{ \alpha ^ i \cdot |S| }[/math]. Therefore, the maximal recursive depth is [math]\displaystyle{ \lceil \log_{a^{-1}}(n)\rceil }[/math]. Since [math]\displaystyle{ \alpha^{-1} \gt 1 }[/math], the total complexity is in [math]\displaystyle{ O(T\cdot n \log n) }[/math] in the worst case.
For the last statement, the average-case analysis, first note that the number of comparisons alone has the same asymptotic complexity as the algorithm as a whole. Next note that any [math]\displaystyle{ x,y \in S }[/math] are compared at most once throughout the entire algorithm if, and only if, [math]\displaystyle{ x }[/math] or [math]\displaystyle{ y }[/math] is chosen as the pivot value for a subsequence to which both elements belong. For [math]\displaystyle{ x,y \in S }[/math], let [math]\displaystyle{ Pr(x,y) }[/math] denote the probability that [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are indeed compared. Since comparison events are distinct and [math]\displaystyle{ Pr(x,y )\in \{0,1\} }[/math] for all [math]\displaystyle{ x,y \in S }[/math], the expected number of comparisons is
[math]\displaystyle{ \sum_{x,y \in S, x \neq y} Pr(x,y) }[/math]
Let [math]\displaystyle{ n := |S| }[/math], and for [math]\displaystyle{ i,j \in \{1,\dots,n\} }[/math], let [math]\displaystyle{ Pr(i,j) }[/math] denote the probability that the [math]\displaystyle{ i }[/math]-th and the [math]\displaystyle{ j }[/math]-th elemet of the eventual sorted sequence are compared throughout the algorithm. Using this notation, we may rewrite the above summation as follows:
[math]\displaystyle{ \sum_{x,y \in S, x \neq y} Pr(x,y) = \sum_{i=1}^{n-1} \sum_{j = i+1}^{n} Pr(i,j) }[/math].
For [math]\displaystyle{ i,j \in \{1,\dots,n\} }[/math], [math]\displaystyle{ i \lt j }[/math], let [math]\displaystyle{ S_{ij} }[/math] denote the subsequence of the eventual sorted sequence that starts with [math]\displaystyle{ i }[/math] and ends with [math]\displaystyle{ j }[/math]. The elements [math]\displaystyle{ \#i }[/math] and [math]\displaystyle{ \#j }[/math] are compared if, and only if, [math]\displaystyle{ \#i }[/math] or [math]\displaystyle{ \#j }[/math] is the very first element of [math]\displaystyle{ S_{ij} }[/math] to be chosen as a pivot. The probability of this event is [math]\displaystyle{ \frac{2}{|S_{ij}|} = \frac{2}{j - i + 1} }[/math], so we obtain
[math]\displaystyle{ \sum_{i=1}^{n-1} \sum_{j = i+1}^{n} \frac{2}{j-i+1} }[/math].
Substituting [math]\displaystyle{ k := j-i }[/math], this gives
[math]\displaystyle{ \sum_{i=1}^{n-1} \sum_{j = i+1}^{n} \frac{2}{j-i+1} = \sum_{i=1}^{n-1} \sum_{k=1}^{n} \frac{2}{k+1} \leq 2(n - 1) }[/math].
[math]\displaystyle{ \sum_{k=1}^n \frac{1}{k+1} \leq 2(n-1) }[/math].
[math]\displaystyle{ \sum_{k+1}^n \frac{1}{k} }[/math].
The asymptotic behavior of the harmonic series is [math]\displaystyle{ \Theta(\log n) }[/math], so the last expression is [math]\displaystyle{ \Theta(T\cdot n \log n) }[/math].
Further information
If [math]\displaystyle{ S }[/math] is an array, [math]\displaystyle{ S }[/math] cannot be decomposed into subsequences. We would liko to avoid the need for additional arrays and copy operations. Instead, the array should be sorted in-place, that is, by swap operations on pairs of elements. The auxiliary procedure, Pivot partitioning by scanning, is designed exactly for that: it permutes the array such that each of [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_2 }[/math] is a subarray. Then each recursive call of Quicksort operates on a subarray of the input array, which is specified by two index pointers.