Max-Flow Problems: Difference between revisions

From Algowiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(23 intermediate revisions by 3 users not shown)
Line 1: Line 1:
== Assumptions ==
== Basic definitions ==
[[File:MaxFlowexample.png|300px|thumb|right|Max-Flow example graph]]
 
For convenience, without loss of generality:
# [[Basic graph definitions]]
# In all variations below, all numbers are integral: real numbers may be approximated by uniformly distant numbers with a negligible loss of precision.
# [[Basic flow definitions]]
# There are no parallel arcs in directed graphs <math>G=(V,A): </math> if there are parallel arcs, they may be replaced by one of them, with their upper bounds, lower bounds, and flow values summed up, respectively. In particular, an arc may be identified with the ordered pair <math>(v,w)</math> consisting of the arc's tail <math>v\in V</math> and head <math>w\in V</math>.
# For each arc <math>(v,w)\in A</math>, there is also a reverse arc <math>(w,v)\in A</math>: if not, just add one with upper (and lower) bound zero.


== Standard version ==
== Standard version ==
Line 12: Line 10:
# A '''source node''' <math>s\in V</math> and a '''target (a.k.a. sink) node''' <math>t\in V</math>.
# A '''source node''' <math>s\in V</math> and a '''target (a.k.a. sink) node''' <math>t\in V</math>.
# A nonnegative '''upper bound (a.k.a. capacity)''' <math>u(a)</math> for each arc <math>a\in A</math>.
# A nonnegative '''upper bound (a.k.a. capacity)''' <math>u(a)</math> for each arc <math>a\in A</math>.


'''Output:'''
'''Output:'''
A maximum <math>(s,t)</math>-flow, that is, a nonnegative value  <math>f(a)</math> for each arc <math>a\in A</math> such that:
A [[Basic flow definitions#Feasible flow|feasible <math>(s,t)</math>-flow]] that has maximum [[Basic flow definitions#Flow value|flow value]] among all feasible <math>(s,t)</math>-flows.
# The flow is '''feasible''' following two conditions are fulfilled:
## '''Capacity constraint:''' For each arc <math>a\in A</math>, it is <math>f(a)\leq u(a)</math>.
## '''Flow conservation condition:''' For each node <math>v\in V\setminus\{s,t\}</math>, it is
#::<math>\sum_{a=(v,w)\in A}f(a)=\sum_{a=(w,v)\in A}f(a)</math>.
# Among all feasible flows, <math>f</math> has maximum '''flow value''', which is defined as
#:<math>v(f):=\sum_{(s,v)\in A}f(s,v)-\sum_{(v,s)\in A}f(v,s)=\sum_{(v,t)\in A}f(v,t)-\sum_{(t,v)\in A}f(t,v)</math>.


== Known algorithms ==
== Known algorithms ==
Line 36: Line 27:


# For each arc <math>a\in A</math>, there is a '''lower bound''' <math>\ell(a)</math>, and <math>f(a)\geq\ell(a)</math> is additionally required. The lower bounds need not be nonnegative, so the flow values need not be nonnegative, either. This version is often called '''maximum flow with edge demands'''. It may be reduced to solving two instances of the standard version as follows:
# For each arc <math>a\in A</math>, there is a '''lower bound''' <math>\ell(a)</math>, and <math>f(a)\geq\ell(a)</math> is additionally required. The lower bounds need not be nonnegative, so the flow values need not be nonnegative, either. This version is often called '''maximum flow with edge demands'''. It may be reduced to solving two instances of the standard version as follows:
## First, we construct a new graph <math>G'=(V',A')</math> as follows: We add a super-source <math>s'</math> and a super-target <math>t'</math> to <math>V</math>. Next,  for every node <math>v\in V</math>, we add an arc <math>(s,v)</math> and an arc <math>(v,t)</math> to <math>A</math>. Finally we add an arc <math>(t,s)</math> to <math>A</math>, if not in <math>A</math> yet.
## First, we construct a new graph <math>G'=(V',A')</math> as follows: We add a super-source <math>s'</math> and a super-target <math>t'</math> to <math>V</math>. Next,  for every node <math>v\in V</math>, we add an arc <math>(s',v)</math> and an arc <math>(v,t')</math> to <math>A</math>. Finally we add an arc <math>(t,s)</math> to <math>A</math>, if not in <math>A</math> yet.
## For all arcs <math>a\in A</math>, we set <math>\ell'(a):=0</math>. For each node <math>v\in V</math>, we set  
## For all arcs <math>a\in A</math>, we set <math>\ell'(a):=0</math>. For each node <math>v\in V</math>, we set  
##:<math>u'(s,v):=\sum_{(w,v)\in A}\ell(w,v)</math> and <math>u'(v,t):=\sum_{(v,w)\in A} \ell(v,w)</math>.  
##:<math>u'(s',v):=\max\{0,\sum_{(w,v)\in A}\ell(w,v)\}</math> and <math>u'(v,t'):=\max\{0,\sum_{(v,w)\in A} \ell(v,w)\}</math>.  
##:For all arcs <math>a\in A</math>, we set <math>u'(a):=u(a)-\ell(a)</math>. Finally, we set <math>u'(t,s):=+\infty</math>.
##:For all arcs <math>a\in A</math>, we set <math>u'(a):=u(a)-\ell(a)</math>. Finally, we set <math>u'(t,s):=+\infty</math>.
## It is easy to see that there is a feasible <math>(s,t)</math>-flow <math>f</math> in <math>G</math> with respect to <math>\ell</math> and <math>u</math> if, and only if, all arcs <math>(s',\cdot)</math> and <math>(\cdot,t')</math> are saturated. This the case if, and only if, the maximum flow <math>f'</math> in <math>G</math> from <math>s'</math> to <math>t'</math> with respect to <math>\ell'</math> and <math>u'</math> yields a flow of value <math>\sum_{a\in A}\ell(a)</math>.
## If all additional arcs <math>(s',\cdot)</math> and <math>(\cdot,t')</math> are [[Basic flow definitions#Flow-augmenting paths and saturated arcs|saturated]] by some feasible (and obviously maximum) <math>(s',t')</math>-flow <math>f</math>, the values <math>f(a)+\ell(a)</math> on all original arcs of <math>G</math> obviously form a feasible <math>(s,t)</math>-flow in <math>G</math> with respect to <math>\ell</math> and <math>u</math>. On the other hand, if there is a feasible <math>(s,t)</math>-flow <math>f</math> in <math>G</math> with respect to <math>\ell</math> and <math>u</math>, the values <math>f(a)-\ell(a)</math> on all original arcs in <math>G</math> along with saturating flow values on all additional arcs form a feasible (and obviously maximum) <math>(s',t')</math>-flow.
## More specifically, for <math>(v,w)\in A</math>, we set <math>f(v,w):=f'(v,w)+\ell(v,w)</math>.
## Therefore, we may safely terminate the whole procedure if the additional arcs are '''not''' saturated by a maximum <math>(s',t')</math>-flow. Otherwise, we may construct an instance <math>(G'=(V,A'),s,t,u')</math> of the standard version as follows: for each original arc <math>a=(v,w)\in A</math> insert an opposite arc <math>a'=(w,v)</math> and set <math>u'(a):=u(a)-f(a)\geq 0</math> and <math>u'(a'):=f(a)-\ell(a)\geq 0</math> (cf. [[Basic flow definitions#Residual network|residual network]]).[[File:Maxflowmultiplesource.png|350px|thumb|right|Max-Flow Problem with several sources and targets]]
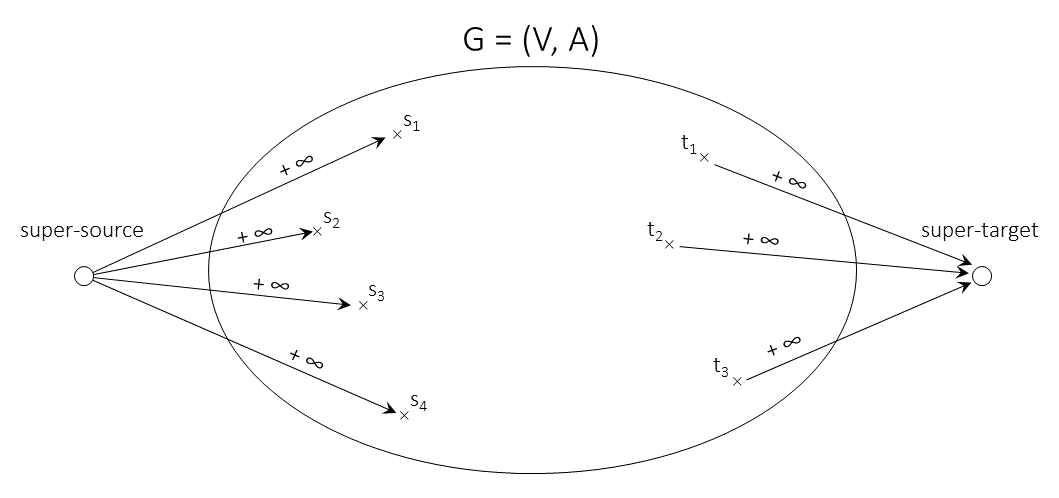
# More than one source and more than one target can be reduced to the standard version by adding a super-source node <math>s</math>, a super-target node <math>t</math>, an arc <math>(s,v)</math> with "infinite" capacity for each source <math>v</math>, and an arc <math>(v,t)</math> with "infinite" capacity for each target <math>v</math>.
# More than one source and more than one target can be reduced to the standard version by adding a super-source node <math>s</math>, a super-target node <math>t</math>, an arc <math>(s,v)</math> with "infinite" capacity for each source <math>v</math>, and an arc <math>(v,t)</math> with "infinite" capacity for each target <math>v</math> (for example, the sum of the upper bounds of all arcs is sufficiently large to serve as "infinity").
# Usually, the term ''generalized flow''' is reserved for the specific generalization in which for each node <math>v\in V\setminus\{vs,t\}</math>, the ratio of the total sum of all incoming flow an the total sum of all outgoing flow is given (in the standard version, this ratio is 1 due to the flow conservation condition).
# Usually, the term '''generalized flow''' is reserved for the specific generalization in which for each node <math>v\in V\setminus\{s,t\}</math>, the ratio of the total sum of all incoming flow and the total sum of all outgoing flow is given (in the standard version, this ratio is 1 due to the flow conservation condition).
# The max-flow problem asks for an optimal steady-state flow. However, in many applications, a certain amount of flow is to be send as soon as possible from the source to the target. It is easy to see that, if the amount of flow is sufficiently large, then an optimal solution is constant most of the time, and the maximum steady-state flow is this constant flow.
# The max-flow problem asks for an optimal steady-state flow. However, in many applications, a certain amount of flow is to be sent as soon as possible from the source to the target. It is easy to see that, if the amount of flow is sufficiently large, then an optimal solution is constant most of the time, and the maximum steady-state flow is this constant flow.

Latest revision as of 08:58, 31 March 2018

Basic definitions

  1. Basic graph definitions
  2. Basic flow definitions

Standard version

Input:

  1. A directed graph [math]\displaystyle{ G=(V,A) }[/math].
  2. A source node [math]\displaystyle{ s\in V }[/math] and a target (a.k.a. sink) node [math]\displaystyle{ t\in V }[/math].
  3. A nonnegative upper bound (a.k.a. capacity) [math]\displaystyle{ u(a) }[/math] for each arc [math]\displaystyle{ a\in A }[/math].

Output: A feasible [math]\displaystyle{ (s,t) }[/math]-flow that has maximum flow value among all feasible [math]\displaystyle{ (s,t) }[/math]-flows.

Known algorithms

  1. Ford-Fulkerson
  2. Edmonds-Karp
  3. Ahuja-Orlin
  4. Dinic
  5. Preflow-push
  6. FIFO preflow-push
  7. Preflow-push with excess scaling

Generalizations

  1. For each arc [math]\displaystyle{ a\in A }[/math], there is a lower bound [math]\displaystyle{ \ell(a) }[/math], and [math]\displaystyle{ f(a)\geq\ell(a) }[/math] is additionally required. The lower bounds need not be nonnegative, so the flow values need not be nonnegative, either. This version is often called maximum flow with edge demands. It may be reduced to solving two instances of the standard version as follows:
    1. First, we construct a new graph [math]\displaystyle{ G'=(V',A') }[/math] as follows: We add a super-source [math]\displaystyle{ s' }[/math] and a super-target [math]\displaystyle{ t' }[/math] to [math]\displaystyle{ V }[/math]. Next, for every node [math]\displaystyle{ v\in V }[/math], we add an arc [math]\displaystyle{ (s',v) }[/math] and an arc [math]\displaystyle{ (v,t') }[/math] to [math]\displaystyle{ A }[/math]. Finally we add an arc [math]\displaystyle{ (t,s) }[/math] to [math]\displaystyle{ A }[/math], if not in [math]\displaystyle{ A }[/math] yet.
    2. For all arcs [math]\displaystyle{ a\in A }[/math], we set [math]\displaystyle{ \ell'(a):=0 }[/math]. For each node [math]\displaystyle{ v\in V }[/math], we set
      [math]\displaystyle{ u'(s',v):=\max\{0,\sum_{(w,v)\in A}\ell(w,v)\} }[/math] and [math]\displaystyle{ u'(v,t'):=\max\{0,\sum_{(v,w)\in A} \ell(v,w)\} }[/math].
      For all arcs [math]\displaystyle{ a\in A }[/math], we set [math]\displaystyle{ u'(a):=u(a)-\ell(a) }[/math]. Finally, we set [math]\displaystyle{ u'(t,s):=+\infty }[/math].
    3. If all additional arcs [math]\displaystyle{ (s',\cdot) }[/math] and [math]\displaystyle{ (\cdot,t') }[/math] are saturated by some feasible (and obviously maximum) [math]\displaystyle{ (s',t') }[/math]-flow [math]\displaystyle{ f }[/math], the values [math]\displaystyle{ f(a)+\ell(a) }[/math] on all original arcs of [math]\displaystyle{ G }[/math] obviously form a feasible [math]\displaystyle{ (s,t) }[/math]-flow in [math]\displaystyle{ G }[/math] with respect to [math]\displaystyle{ \ell }[/math] and [math]\displaystyle{ u }[/math]. On the other hand, if there is a feasible [math]\displaystyle{ (s,t) }[/math]-flow [math]\displaystyle{ f }[/math] in [math]\displaystyle{ G }[/math] with respect to [math]\displaystyle{ \ell }[/math] and [math]\displaystyle{ u }[/math], the values [math]\displaystyle{ f(a)-\ell(a) }[/math] on all original arcs in [math]\displaystyle{ G }[/math] along with saturating flow values on all additional arcs form a feasible (and obviously maximum) [math]\displaystyle{ (s',t') }[/math]-flow.
    4. Therefore, we may safely terminate the whole procedure if the additional arcs are not saturated by a maximum [math]\displaystyle{ (s',t') }[/math]-flow. Otherwise, we may construct an instance [math]\displaystyle{ (G'=(V,A'),s,t,u') }[/math] of the standard version as follows: for each original arc [math]\displaystyle{ a=(v,w)\in A }[/math] insert an opposite arc [math]\displaystyle{ a'=(w,v) }[/math] and set [math]\displaystyle{ u'(a):=u(a)-f(a)\geq 0 }[/math] and [math]\displaystyle{ u'(a'):=f(a)-\ell(a)\geq 0 }[/math] (cf. residual network).
      Max-Flow Problem with several sources and targets
  2. More than one source and more than one target can be reduced to the standard version by adding a super-source node [math]\displaystyle{ s }[/math], a super-target node [math]\displaystyle{ t }[/math], an arc [math]\displaystyle{ (s,v) }[/math] with "infinite" capacity for each source [math]\displaystyle{ v }[/math], and an arc [math]\displaystyle{ (v,t) }[/math] with "infinite" capacity for each target [math]\displaystyle{ v }[/math] (for example, the sum of the upper bounds of all arcs is sufficiently large to serve as "infinity").
  3. Usually, the term generalized flow is reserved for the specific generalization in which for each node [math]\displaystyle{ v\in V\setminus\{s,t\} }[/math], the ratio of the total sum of all incoming flow and the total sum of all outgoing flow is given (in the standard version, this ratio is 1 due to the flow conservation condition).
  4. The max-flow problem asks for an optimal steady-state flow. However, in many applications, a certain amount of flow is to be sent as soon as possible from the source to the target. It is easy to see that, if the amount of flow is sufficiently large, then an optimal solution is constant most of the time, and the maximum steady-state flow is this constant flow.
Retrieved from "https://wiki.algo.informatik.tu-darmstadt.de/index.php?title=Max-Flow_Problems&oldid=3886"