Category:Minimal Spanning Tree: Difference between revisions
Jump to navigation
Jump to search
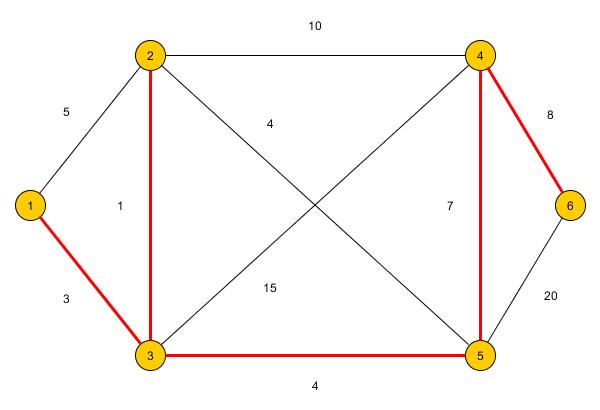
(Created page with "== Introduction == 400px The red colored edges are the minimal spanning tree of this graph. == Input == * A undirected connected graph <math>G=(...") |
(→Output) |
||
| Line 12: | Line 12: | ||
== Output == | == Output == | ||
A acylic subset <math>T \ | A acylic subset <math>T \subseteq E</math> in which <math>w(T) = \sum_{(u,v) \in T} w(u,v)</math> is minimal. | ||
== Generic algorihm == | == Generic algorihm == | ||
Latest revision as of 15:49, 7 November 2014
Introduction
The red colored edges are the minimal spanning tree of this graph.
Input
- A undirected connected graph [math]\displaystyle{ G=(V,E) }[/math]
- A weight [math]\displaystyle{ w(u,v) }[/math] for each edge [math]\displaystyle{ (u,v) \in E }[/math]
Output
A acylic subset [math]\displaystyle{ T \subseteq E }[/math] in which [math]\displaystyle{ w(T) = \sum_{(u,v) \in T} w(u,v) }[/math] is minimal.
Generic algorihm
Generic-MST(G, w)
1 A ← ∅
2 while A is not a spanning tree
3 do determine a edge (u,v)
4 A ← A ∪ {(u,v)}
5 return A
Known algorithms
This category currently contains no pages or media.