Binary search tree: Difference between revisions
Jump to navigation
Jump to search
(→Remark) |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category: | [[Category:Videos]] | ||
[[Category:Data Structures]] | [[Category:Data Structures]] | ||
[[Category:Trees]] | [[Category:Trees]] | ||
[[Category:Binary_Search_Tree]] | [[Category:Binary_Search_Tree]] | ||
{{#ev:youtube|https://www.youtube.com/watch?v=AdhRIRgVZVw|500|right|Binary search tree|frame}} | |||
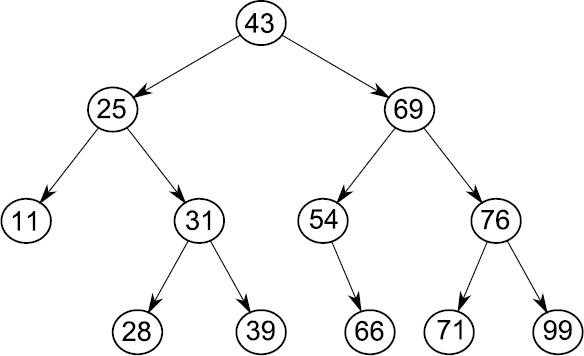
[[File:Bst.png|300px|thumb|right|Simple Binary Search tree]] | [[File:Bst.png|300px|thumb|right|Simple Binary Search tree]] | ||
== General Information == | == General Information == | ||
| Line 25: | Line 17: | ||
# An object of the binary search tree type contains a pointer '''''root''''' of type "pointer to tree item of type <math>\mathcal{K}</math>." | # An object of the binary search tree type contains a pointer '''''root''''' of type "pointer to tree item of type <math>\mathcal{K}</math>." | ||
# The pointer '''''root''''' points to a well-formed binary search tree. In accordance with the definition of [[Directed Tree|directed trees]], "well-formed" means that, for any node, there is exactly one [[Basic graph definitions#Paths|path]] from the root to that node. | # The pointer '''''root''''' points to a well-formed binary search tree. In accordance with the definition of [[Directed Tree|directed trees]], "well-formed" means that, for any node, there is exactly one [[Basic graph definitions#Paths|path]] from the root to that node. | ||
# For each node <math>x</math> in the tree, no key in the left subtree of that node is greater than the key of <math>x</math>, and no key in the right subtree of <math>x</math> is less than the key of <math>x</math>. | |||
== Remark == | == Remark == | ||
* Besides the methods of [[Sorted sequence|sorted sequences]], binary search trees in the implementation chosen here have a private method [[Binary Search Tree:Remove node]], which receives a pointer <math>p</math> to a binary search tree node and removes | * Besides the methods of [[Sorted sequence|sorted sequences]], binary search trees in the implementation chosen here have a private method [[Binary Search Tree:Remove node]], which receives a pointer <math>p</math> to a binary search tree node and removes it (possibly by removing another node and overwriting the key to be removed with the key of the other node. Prerequisite: <math> p</math>.left <math>\neq</math>void. | ||
* There are variants on binary search trees, such as [http://en.wikipedia.org/wiki/AVL_tree AVL trees] and [http://en.wikipedia.org/wiki/Red_black_tree red-black-trees], for which the height of the tree is guaranteed to be in <math>O \log{n}</math> | * There are variants on binary search trees, such as [http://en.wikipedia.org/wiki/AVL_tree AVL trees] and [http://en.wikipedia.org/wiki/Red_black_tree red-black-trees], for which the height of the tree is guaranteed to be in <math>O(\log{n})</math> at any time (because the additional operations to maintain logarithmic height are linear in the height of the tree as well). | ||
* The mathematical concept behind this data structure is described in the section on [[Directed Tree#Binary Search Tree|binary search trees]] of page [[Directed Tree]]. | * The mathematical concept behind this data structure is described in the section on [[Directed Tree#Binary Search Tree|binary search trees]] of page [[Directed Tree]]. | ||
Latest revision as of 06:14, 6 July 2015
General Information
Abstract data structure: Sorted sequence
Implementation invariant:
- There is a tree item type with three components:
- key is of generic type [math]\displaystyle{ \mathcal{K} }[/math],
- left and right of type "pointer to tree item of type [math]\displaystyle{ \mathcal{K} }[/math]."
- An object of the binary search tree type contains a pointer root of type "pointer to tree item of type [math]\displaystyle{ \mathcal{K} }[/math]."
- The pointer root points to a well-formed binary search tree. In accordance with the definition of directed trees, "well-formed" means that, for any node, there is exactly one path from the root to that node.
- For each node [math]\displaystyle{ x }[/math] in the tree, no key in the left subtree of that node is greater than the key of [math]\displaystyle{ x }[/math], and no key in the right subtree of [math]\displaystyle{ x }[/math] is less than the key of [math]\displaystyle{ x }[/math].
Remark
- Besides the methods of sorted sequences, binary search trees in the implementation chosen here have a private method Binary Search Tree:Remove node, which receives a pointer [math]\displaystyle{ p }[/math] to a binary search tree node and removes it (possibly by removing another node and overwriting the key to be removed with the key of the other node. Prerequisite: [math]\displaystyle{ p }[/math].left [math]\displaystyle{ \neq }[/math]void.
- There are variants on binary search trees, such as AVL trees and red-black-trees, for which the height of the tree is guaranteed to be in [math]\displaystyle{ O(\log{n}) }[/math] at any time (because the additional operations to maintain logarithmic height are linear in the height of the tree as well).
- The mathematical concept behind this data structure is described in the section on binary search trees of page Directed Tree.