Big O notation: Difference between revisions
Jump to navigation
Jump to search
(Created page with "<math>x^{a+b}</math>") |
m (Luedecke moved page Asymptotic notation to Big O notation) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<math> | |||
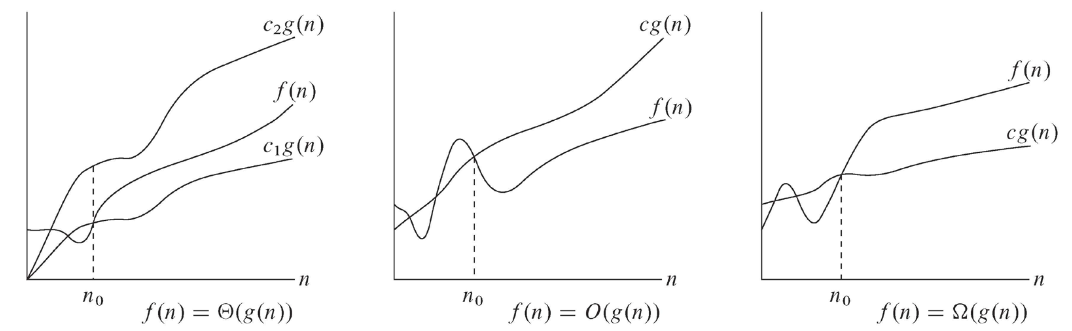
:<math>\Theta(g(n)) = \{f(n) :</math> there exist positive constants <math>c_1</math>,<math>c_2</math> and <math>n_0</math> such that <math>0\le \;c_1g(n) \le \; f(n) \le \; c_2g(n)</math> for all <math>n \ge \; n_0 \}</math> | |||
:<math>O(g(n)) = \{f(n) :</math> there exist positive constants <math>c</math> and <math>n_0</math> such that <math>0\le \; f(n) \le \; cg(n)</math> for all <math>n \ge \; n_0 \}</math> | |||
:<math>\Omega(g(n)) = \{f(n) :</math> there exist positive constants <math>c</math> and <math>n_0</math> such that <math>0 \le \; cg(n)\le \; f(n)</math> for all <math>n \ge \; n_0 \}</math> | |||
:<math>o(g(n)) = \{f(n) :</math> for any positive constant <math>c > 0</math>, there exists ac constant <math>n_0 > 0</math> such that <math>0 \le \; f(n) < cg(n)</math> for all <math>n \ge \; n_0 \}</math> | |||
[[File:anots.png]] | |||
Latest revision as of 16:04, 18 October 2014
- [math]\displaystyle{ \Theta(g(n)) = \{f(n) : }[/math] there exist positive constants [math]\displaystyle{ c_1 }[/math],[math]\displaystyle{ c_2 }[/math] and [math]\displaystyle{ n_0 }[/math] such that [math]\displaystyle{ 0\le \;c_1g(n) \le \; f(n) \le \; c_2g(n) }[/math] for all [math]\displaystyle{ n \ge \; n_0 \} }[/math]
- [math]\displaystyle{ O(g(n)) = \{f(n) : }[/math] there exist positive constants [math]\displaystyle{ c }[/math] and [math]\displaystyle{ n_0 }[/math] such that [math]\displaystyle{ 0\le \; f(n) \le \; cg(n) }[/math] for all [math]\displaystyle{ n \ge \; n_0 \} }[/math]
- [math]\displaystyle{ \Omega(g(n)) = \{f(n) : }[/math] there exist positive constants [math]\displaystyle{ c }[/math] and [math]\displaystyle{ n_0 }[/math] such that [math]\displaystyle{ 0 \le \; cg(n)\le \; f(n) }[/math] for all [math]\displaystyle{ n \ge \; n_0 \} }[/math]
- [math]\displaystyle{ o(g(n)) = \{f(n) : }[/math] for any positive constant [math]\displaystyle{ c \gt 0 }[/math], there exists ac constant [math]\displaystyle{ n_0 \gt 0 }[/math] such that [math]\displaystyle{ 0 \le \; f(n) \lt cg(n) }[/math] for all [math]\displaystyle{ n \ge \; n_0 \} }[/math]