Branching by Edmonds

Abstract view

Algorithmic problem: Maximum branching

Definition:

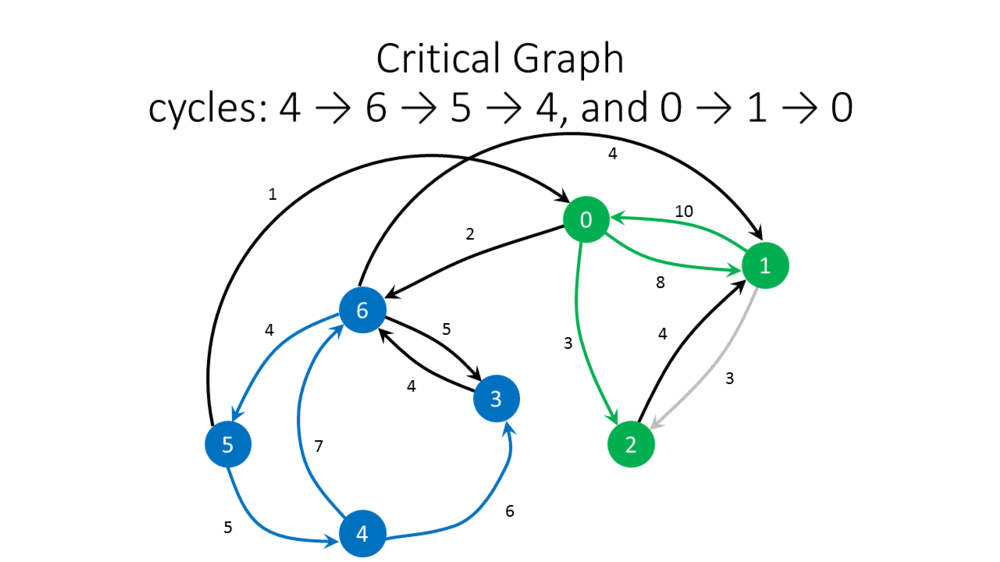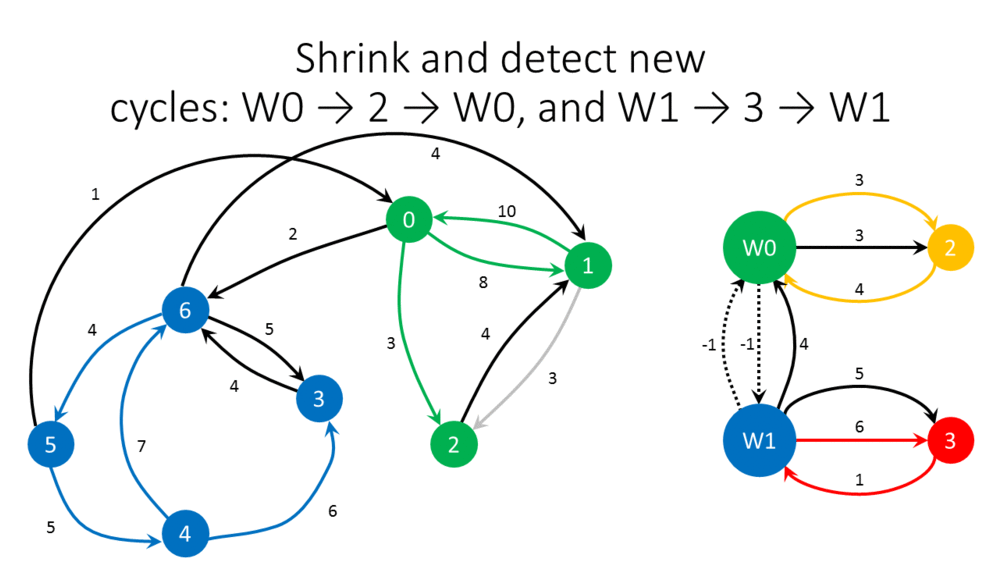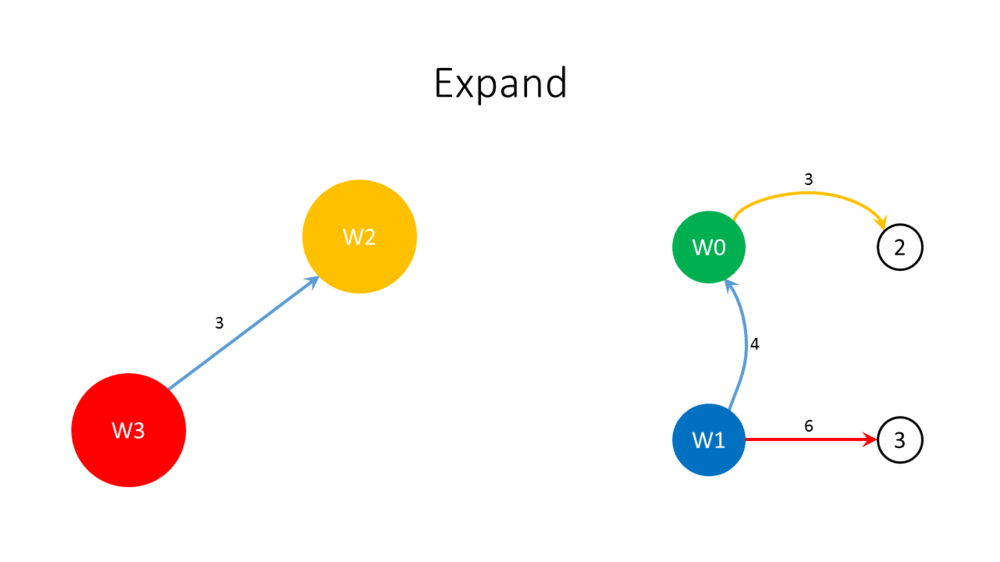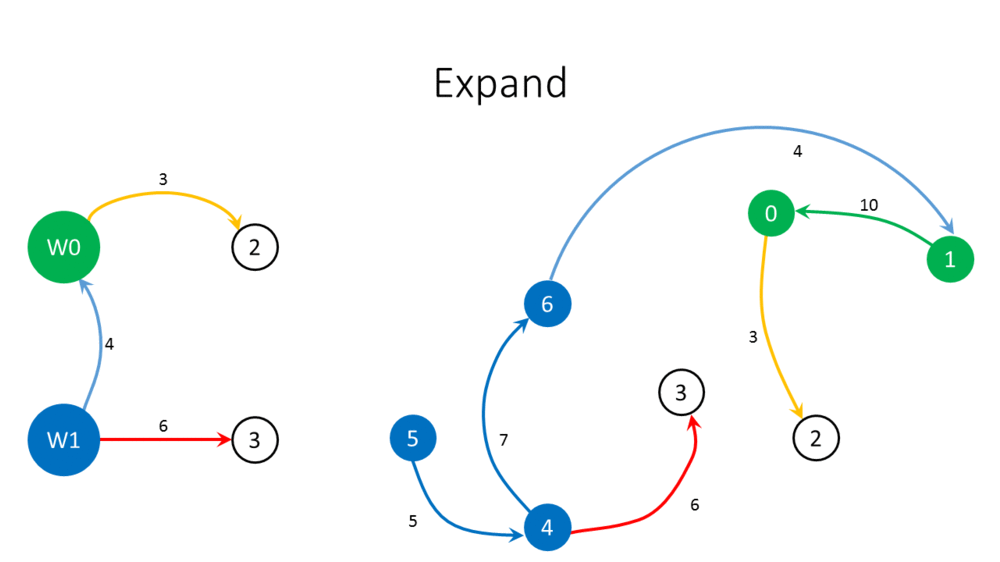
1. An arc [math]\displaystyle{ (v,w)\in A }[/math] is critical for [math]\displaystyle{ w\in V }[/math] if its weight is not smaller than the weight of any other incoming arc of [math]\displaystyle{ w }[/math].
2. A critical subgraph [math]\displaystyle{ G'=(V,A') }[/math] of [math]\displaystyle{ G }[/math] contains exactly one incoming arc [math]\displaystyle{ (v,w)\in A }[/math] for each node [math]\displaystyle{ w\in V }[/math] of positive indegree, where [math]\displaystyle{ (v,w) }[/math] is critical.

Type of algorithm: recursion

Invariant: The output of a recursive call is a maximum branching of the weighted graph that was the input for this recursive call.

Recursion anchor

Abstract view: Terminate if [math]\displaystyle{ G' }[/math] is cycle-free.

Proof: If [math]\displaystyle{ G' }[/math] is cycle-free, it is a branching. Consider some other branching [math]\displaystyle{ B }[/math]. We have to show that [math]\displaystyle{ B }[/math] does not have more total weight than [math]\displaystyle{ G' }[/math].

By definition, a critical graph contains one incoming arc for each node that does have incoming arcs. Therefore, for each arc [math]\displaystyle{ a }[/math] of [math]\displaystyle{ B }[/math], there is an arc [math]\displaystyle{ a' }[/math] in [math]\displaystyle{ G' }[/math] pointing to the same node. Due to the choice of arcs for [math]\displaystyle{ G' }[/math], it is [math]\displaystyle{ w(a)\leq w(a') }[/math].

Recursive step

animated gif: Branching by Edmonds

Abstract view:

1. Compute a critical subgraph [math]\displaystyle{ G'=(V,A') }[/math] for the input graph [math]\displaystyle{ G }[/math].
2. Identify some cycle [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G' }[/math].
3. Let [math]\displaystyle{ W }[/math] denote the minimum weight of all arcs on [math]\displaystyle{ C }[/math].
4. For every arc [math]\displaystyle{ (v,w)\in A }[/math] pointing from some node [math]\displaystyle{ v }[/math] outside [math]\displaystyle{ C }[/math] to some node [math]\displaystyle{ w }[/math] on [math]\displaystyle{ C }[/math]:
   1. Decrease the weight of [math]\displaystyle{ (v,w) }[/math] by [math]\displaystyle{ w(v',w)-W\geq 0 }[/math], where [math]\displaystyle{ (v',w) }[/math] is the incoming arc of [math]\displaystyle{ w }[/math] on [math]\displaystyle{ C }[/math].
   2. If the new weight of [math]\displaystyle{ (v,w) }[/math] is not positive, remove [math]\displaystyle{ (v,w) }[/math] from [math]\displaystyle{ G }[/math].
5. Shrink [math]\displaystyle{ C }[/math] into one new super-node, where every arc pointing to (resp., from) some node on [math]\displaystyle{ C }[/math] now points to (from) that super-node.
6. Call the algorithm recursively for the modified weighted graph after shrinking, giving branching [math]\displaystyle{ B }[/math].
7. Unshrink the graph.
8. Add all arcs of [math]\displaystyle{ C }[/math] to [math]\displaystyle{ B }[/math] giving [math]\displaystyle{ B' }[/math].
9. If [math]\displaystyle{ B' }[/math] contains an arc [math]\displaystyle{ (v,w) }[/math] such that [math]\displaystyle{ v }[/math] is outside [math]\displaystyle{ C }[/math] and [math]\displaystyle{ w }[/math] is on [math]\displaystyle{ C }[/math]: remove the incoming arc of [math]\displaystyle{ w }[/math] on [math]\displaystyle{ C }[/math] from [math]\displaystyle{ B }[/math]; otherwise, remove one arc with weight [math]\displaystyle{ W }[/math] on [math]\displaystyle{ C }[/math]. Let [math]\displaystyle{ B'' }[/math] be the result in both cases.
10. Return [math]\displaystyle{ B'' }[/math].

Proof: Obviously, [math]\displaystyle{ B'' }[/math] is a branching, so we have to prove that it has maximum weight among all branchings in [math]\displaystyle{ G }[/math]. Let [math]\displaystyle{ B_{\mathrm{opt}} }[/math] be a maximum branching in [math]\displaystyle{ G }[/math] such that, among all maximum branchings in [math]\displaystyle{ G }[/math], [math]\displaystyle{ B_{\mathrm{opt}} }[/math] shares as many arcs as possible with [math]\displaystyle{ B'' }[/math].

Let [math]\displaystyle{ C' }[/math] be a cycle of [math]\displaystyle{ G' }[/math] (the case [math]\displaystyle{ C'=C }[/math] not excluded). First we show that [math]\displaystyle{ B_{\mathrm{opt}} }[/math] contains all arcs of [math]\displaystyle{ C' }[/math] except one. So, suppose for a contradiction that [math]\displaystyle{ B_{\mathrm{opt}} }[/math] does not contain some of the arcs of [math]\displaystyle{ C' }[/math], say, [math]\displaystyle{ (v_1,w_1),\ldots,(v_k,w_k) }[/math] with [math]\displaystyle{ k\gt 1 }[/math].

Replacing the incoming arc of any [math]\displaystyle{ w_i }[/math] by [math]\displaystyle{ (v_i,w_i) }[/math] in [math]\displaystyle{ B_{\mathrm{opt}} }[/math] and doing nothing else, would not decrease the total weight. Since [math]\displaystyle{ B_{\mathrm{opt}} }[/math] is as close as possible to [math]\displaystyle{ B'' }[/math], such a replacement cannot result in a branching anymore. Since the indegrees do not change by that replacement, this means that adding [math]\displaystyle{ (v_i,w_i) }[/math] to [math]\displaystyle{ B_{\mathrm{opt}} }[/math] would close a cycle. In other words, there is a path [math]\displaystyle{ p_i }[/math] in [math]\displaystyle{ B_{\mathrm{opt}} }[/math] from [math]\displaystyle{ w_i }[/math] to [math]\displaystyle{ v_i }[/math]. Each path [math]\displaystyle{ p_i }[/math] must enter [math]\displaystyle{ C' }[/math] at one of the nodes [math]\displaystyle{ w_j }[/math] because, otherwise, the node where [math]\displaystyle{ p_i }[/math] enters [math]\displaystyle{ C' }[/math] had two incoming arcs in [math]\displaystyle{ B_{\mathrm{opt}} }[/math]: the incoming arc on [math]\displaystyle{ C' }[/math] and the arc over which [math]\displaystyle{ p_i }[/math] enters [math]\displaystyle{ C' }[/math]. However, this would imply that there is a cycle in the union of all paths [math]\displaystyle{ p_i }[/math]. This union is a subset of [math]\displaystyle{ B_{\mathrm{opt}} }[/math], which yields the desired contradiction.

Now we know that [math]\displaystyle{ B_{\mathrm{opt}} }[/math] contains all arcs except one on all cycles of [math]\displaystyle{ G' }[/math]. Note that, for any node not on a cycle, the incoming branching arc may be freely chosen without any effect on the rest. So, since [math]\displaystyle{ B_{\mathrm{opt}} }[/math] is as close as possible to [math]\displaystyle{ B'' }[/math],[math]\displaystyle{ B_{\mathrm{opt}} }[/math] and [math]\displaystyle{ B'' }[/math] agree on all of these choices. Further note that all cycles of [math]\displaystyle{ G' }[/math] are node-disjoint. In summary, we may compare [math]\displaystyle{ B_{\mathrm{opt}} }[/math] and [math]\displaystyle{ B'' }[/math] on each cycle of [math]\displaystyle{ G' }[/math] separately.

For [math]\displaystyle{ C }[/math], complete agreement between [math]\displaystyle{ B_{\mathrm{opt}} }[/math] and [math]\displaystyle{ B'' }[/math] follows from the observation that the choice of incoming arcs for all nodes on [math]\displaystyle{ C }[/math] is optimal in [math]\displaystyle{ B'' }[/math] due to the specific modification of the arc weights. And for all other cycles of [math]\displaystyle{ G' }[/math], complete agreement follows from the induction hypothesis. In both cases, we again used the specific choice of [math]\displaystyle{ B_{\mathrm{opt}} }[/math] to be as close to [math]\displaystyle{ B'' }[/math] as possible.

Complexity

Statement: The asymptotic complexity is in [math]\displaystyle{ \mathcal{O}((n+m)\cdot n) }[/math] in the worst case, where [math]\displaystyle{ n=|V| }[/math] and [math]\displaystyle{ m=|A| }[/math].

Proof: Using DFS for cycle detection, each recursive step requires [math]\displaystyle{ \mathcal{O}(n+m) }[/math]. In each shrink operation, the number of nodes decreases, so the recursion depth is [math]\displaystyle{ \mathcal{O}(n) }[/math].

Remark: More sophisticated implementations of this algorithm yield better asymptotic complexities.

Remarks

1. The unshrink operation requires that the shrink operation performs some bookkeeping: For the super-node, a cyclically ordered sequence of all nodes and arcs on [math]\displaystyle{ C }[/math] (or an equivalent bulk of information) must be attached to a super-node.
2. Several cycles may be discovered simultaneously by one run of DFS. Note that all cycles in a critical graph are node-disjoint, because no node has more than one incoming arc. Therefore, several cycles may be handled in the same recursive call, without any interference.