Big O notation: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
:<math>o(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that 0<=''c''<sub>1</sub>*g(n) <= f(n) <= c2*g(n) for all >= n0 }</math> | :<math>o(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that 0<=''c''<sub>1</sub>*g(n) <= f(n) <= c2*g(n) for all >= n0 }</math> | ||
[[File:anots. | [[File:anots.png]] | ||
Revision as of 00:50, 10 September 2014
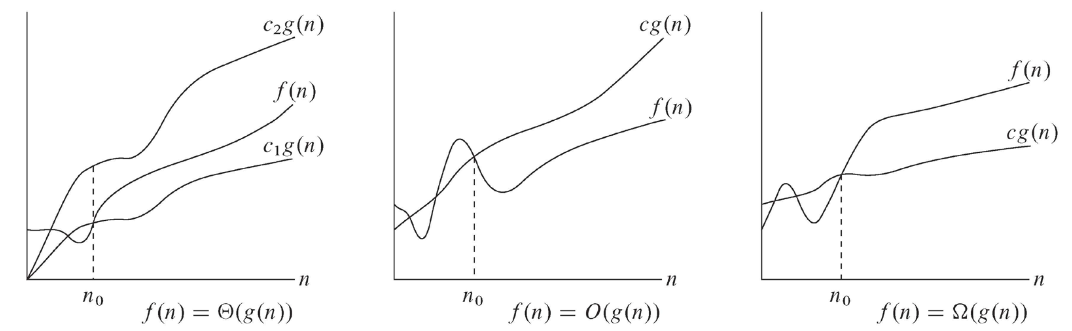
- [math]\displaystyle{ \Theta(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that 0\lt =''c''\lt sub\gt 1\lt /sub\gt *g(n) \lt = f(n) \lt = c2*g(n) for all \gt = n0 } }[/math]
- [math]\displaystyle{ O(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that 0\lt =''c''\lt sub\gt 1\lt /sub\gt *g(n) \lt = f(n) \lt = c2*g(n) for all \gt = n0 } }[/math]
- [math]\displaystyle{ \Omega(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that 0\lt =''c''\lt sub\gt 1\lt /sub\gt *g(n) \lt = f(n) \lt = c2*g(n) for all \gt = n0 } }[/math]
- [math]\displaystyle{ o(g(n)) = {f(n) : there exist positive constants c1,c2 and n0 such that 0\lt =''c''\lt sub\gt 1\lt /sub\gt *g(n) \lt = f(n) \lt = c2*g(n) for all \gt = n0 } }[/math]