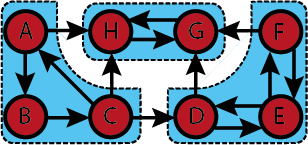
Strongly connected components

Definition

Graph with marked strongly connected components

Let [math]\displaystyle{ G=(V,A) }[/math] be a directed graph. Consider the following equivalence relation on the nodes: [math]\displaystyle{ v\in V }[/math] and [math]\displaystyle{ w\in V }[/math] are equivalent if, and only if, there is a path fmo [math]\displaystyle{ v }[/math] to [math]\displaystyle{ w }[/math] and a path from [math]\displaystyle{ w }[/math] to [math]\displaystyle{ v }[/math] in [math]\displaystyle{ G }[/math]. The equivalence classes are called the strongly connected components (SCC) of [math]\displaystyle{ G }[/math].

Input

A directed graph [math]\displaystyle{ G=(V,A) }[/math].

Output

A set of sets of nodes. Each set of nodes contains exactly the nodes of one SCC. The correspndence between SCC and sets of nodes is one-to-one.