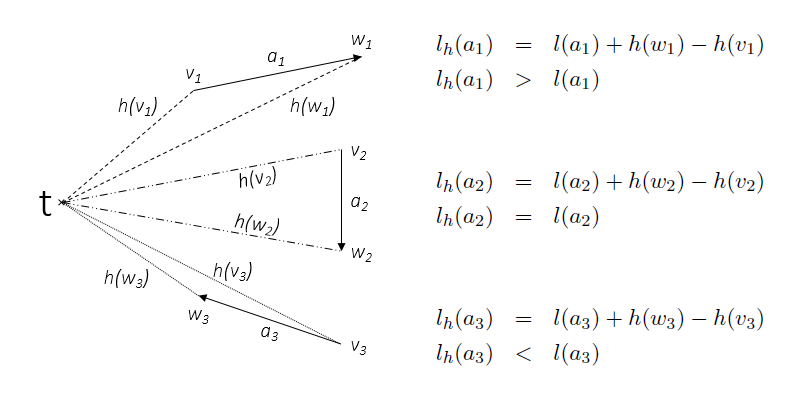Dijkstra

Chapters

1. [00:00] Einführung
2. [05:33] Ändern sich die Pfade stark in jeder Iteration?
3. [06:08] Auf was für Strukturen arbeiten wir eigentlich?
4. [07:26] Distanzen und kürzeste Pfade
5. [10:59] Varianten des Kürzeste-Pfade-Problems
6. [14:00] Dijkstra implementiert
7. [16:00] Wieso funktioniert dieser Algorithmus, warum ist er korrekt?
8. [21:28] Was gibt es zum Preprocessing bzw. Induktionsanfang zu sagen?
9. [21:57] Was ist in der Queue?
10. [22:15] Was wissen wir über die erledigten Knoten?
11. [23:00] Und was wissen wir über die unerledigten Knoten?
12. [23:49] Und was ist mit der asymptotischen Komplexität?

General information

Algorithmic problem: Single source shortest paths

Prerequisities: For all $\alpha \in A$, it is $l(a)\ge 0$.

Type of algortihm: loop

Auxiliary data:

1. A temporary distance value $\delta (v)\in \mathbb{R}$ for each node $v\in V$. At termination, it is $\delta (v)=\mathrm{\Delta }(v)$ for all $v\in V$ where $\mathrm{\Delta }(v)$ is the shortest $(s,v)$-path.
2. A bounded priority queue $Q$ of size $|V|-1$, which contains nodes from $V$ and takes their $\delta$-values as keys. The node with minimal key is returned.

Abstract view

Invariant: After $i\ge 0$ iterations:

1. $Q$ contains all nodes of $V$ except $s$ and $i$ further nodes.
2. For the nodes $v\in V$ not in $Q$, it is $\delta (v)=\mathrm{\Delta }(v)$.
3. For the nodes $v\in V$ in $Q$, $\delta (v)$ is the length of a shortest $(s,v)$-path that solely contains nodes not in $Q$ (except for $v$ itself, of course). As usual, this means $\delta (v)=+\mathrm{\infty }$ if there is no such path.

In particular, it is $\delta (v)\ge \mathrm{\Delta }(v)$ for each node $v\in V$.

Variant: $i$ increases by $1$.

Break condition:

• $Q=\mathrm{\varnothing }$, which means that all nodes are reachable from $s$ and have been processed;
• otherwise, if $\delta (v)=+\mathrm{\infty }$ for the next node $v$ of $Q$, which means that $\delta (v)=+\mathrm{\infty }$ for every node in $Q$ and hence none of the nodes in $Q$ is reachable from $s$.

Induction basis

Abstract view:

1. All nodes of $V$ except $s$ have to be members of $Q$.
2. Root $s$ must have correct distance $\mathrm{\Delta }(s)=0$.
3. The other nodes must meet Invariant #3.

Implementation:

1. $\delta (s):=0$;
2. For all $a=(s,v)\in A$, set $\delta (v):=l(a)$.
3. For all $v\in V\setminus \{s\}$ with $(s,v)\notin A$ set $\delta (v):=+\mathrm{\infty }$.
4. Insert all nodes in $V\setminus \{s\}$ into $Q$.

Proof:

Obvious.

Induction step

Abstract view:

One node is extracted from $Q$, and the distance values of the endnodes of its outgoing arcs are updated to meet Invariant #3.

Implementation:

1. Extract the next node $v$ from $Q$.
2. For each outgoing arc $a=(v,w)\in A$ such that $w\in Q$, set $\delta (w):=min\{\delta (w),\delta (v)+l(a)\}$.

Correctness:

The first invariant is trivially maintained. So we will focus on the second and third invariants.
Consider the moment immediately before the $i$-iteration. The core of the proof is to show that $\delta (v)=\mathrm{\Delta }(v)$ hold at that moment (and hence forever). For a contradiction, suppose there is an $(s,v)$-path $p$ whose length is strictly less than $\delta (v)$. The third invariant implies that $p$ has nodes in $Q$ beside $v$. Let $u$ denote the first such node on $p$. Then none of the nodes on the subpath of $p$ from $s$ to $u$ belonged to $Q$ at that moment (except for $u$ itself, of course). Due to the prefix property, this subpath is a shortest $(s,u)$-path, so Invariant #3 implies $\delta (u)=\mathrm{\Delta }(u)$. On the other hand, the specific choice of $v$ implies $\delta (u)\ge \delta (v)$. In summary, the subpath of $p$ from $s$ to $w$ is not shorter than $\delta (v)$. To obtain $l(p)<\delta (v)$, the subpath of $p$ from $u$ to $v$ must have negative total length, which contradicts the prerequisite $l\ge 0$.
Now we know $\delta (v)=\mathrm{\Delta }(v)$. Therefore, $v$ fulfills the statement of the second invariant after the $i$-th iteration. Of course, the second invariant is not violated by any other node either, and is thus maintained.
For a node $w\in V$ let $P_i(w)$ denote the set of all $(s,w)$-paths such that no node (except for $w$ itself) is in $Q$ immediately after the $i$-th iteration. In particular, the statement of the third invariant means that $\delta (w)$ is the length of a shortest path in $P_i(w)$. The induction hypothesis says that $\delta (w)$ is the minimum length of all $(s,w)$-paths in $P_{i-1}(w)$. The difference $P_i(w)\setminus P_{i-1}(w)$ consists of all $(s,w)$-paths such that $(v,w)$ is the last arc and all nodes except for $v$ and $w$ belong to $V_{i-1}$. Therefore, the second step of the iteration incorporates $P_i(w)\setminus P_{i-1}(w)$ in the computation of $\delta (w)$ appropriately to maintain Invaraint #3.

Complexity

Statement: The worst-case complexity is in $O(T(n)\cdot (n+m))$, where $n=|V|$ and $m=|A|$, and $T(n)$ is the worst-case complexity for extraction/inserting nodes in $Q$.

Proof: Each node is inserted in and extracted from $Q$ at most once, respectively, which gives $O(T(n)\cdot n)$ in total. Also, each arc $(v,w)\in A$ is touched at most once, namely

• in the initialization if $v=s$,
• when $v$ is extracted from $Q$ otherwise.

Therefore, all decrease-key operations require $O(T(n)\cdot m)$ in total.

Pseudocode

DIJKSTRA(G,w,s)

DIJKSTRA(G,w,s)
1 INITIALIZE-SINGLE-SOURCE(G,s) 
2      S = ∅
3      Q = G.V
4      while Q ≠ ∅
5            u = EXTRACT-MIN(Q)
6            S = S ∪ {u} 
7            for each vertex v ∈ G.Adj[u]
8                 RELAX(u,v,w)

RELAX(u,v,w)

RELAX(u,v,w)
1 if v.d > u.d + w(u,v)
2       v.d = u.d + w(u,v)
3       v.π = u

INITIALIZE-SINGLE-SOURCE(G,s)

INITIALIZE-SINGLE-SOURCE(G,s) 
1 for each vertex v ∈ G.V
2         v.d = ∞
3         v.π = NIL
4 s.d = 0

Heuristic speed-up techniques

1. We do not need to insert all nodes except for $s$ in $Q$. In fact, it suffices to initially insert the endnodes of the outgoing arcs of $s$ and, during an iteration, to insert the nodes of the outgoing arcs of the node that is being extracted from $Q$. In a sense, the nodes of $Q$ then constitute the "frontierline" of the algorithm. We choose another variant on Dijkstra's algorithm mainly for simplicity of presentation.
2. Clearly, Dijkstra's algorithm also solves the single-source single-target case. In this case, Dijkstra may safely terminate once has been extracted from $Q$. In fact, the loop invariant implies $\delta (t)=\mathrm{\Delta }(t)$ from then on. This variant on Dijkstra's algorithm is sometimes called the early termination variant.
   

   advantage of a bidirectional search
3. In the single-source single-target case, two searches may be applied simultaneously: one from $s$ on $G$, the other one from $t$ on the transpose of $G$. This variant is called bidirectional search. It terminates once one node has been seen by both searches. Then either the concatenation of the paths to this node from both searches is a shortest $(s,t)$-path, or such a path may be found among the paths of the following kind: There is an arc $(v,w)\in A$ such that $v$ has been seen in the forward search from the source and $w$ has been seen in the backward search from $t$.
4. In a scenario where we perform a large number of searches on the same graph and arc lengths, we do not need to touch the whole graph in each search:
   1. We change the algorithm as suggested by the first point: only keep the "frontierline" in $Q$.
   2. We also change the algorithm as suggested by the second point: terminate once $t$ is processed.
   3. To avoid touching all nodes for initializing the $\delta$-values, we maintain sort of a version counter, or time stamp, for each node, which holds the ID of the last search that met this node. Whenever a node is met in a search and the nodes version counter does not equal the ID of the current search, the distance value of this node is regarded as $+\mathrm{\infty }$ (no matter what its current value is).
      

      the length of a non-goal-directed arc grows, the length of a neutral arc stays the same and the length of the goal-directed arc shriks
5. The early termination variant may be modified as follows: For admissible node potentials $h:V\to \mathbb{R}$, replace length $\ell$ by ${\ell }_h$ where ${\ell }_h(a):=\ell (a)+h(w)-h(v)$ for each $a=(v,w)\in A$. This variant is usually called goal-directed search. The heuristic idea is that we (hopefully) reach $t$ earlier because the arcs that roughly point towards $t$ are shortened, and the arcs the roughly point in a direction away from $t$ are lengthened.