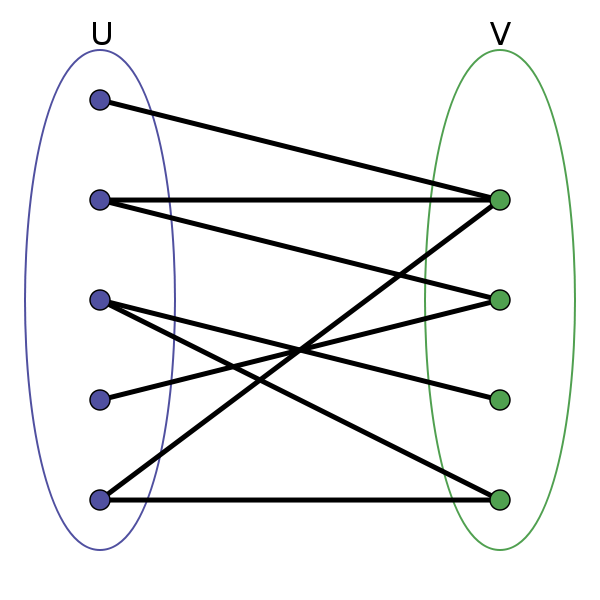
Bipartite graph
Jump to navigation
Jump to search
Definition
An undirected graph [math]\displaystyle{ G=(V,E) }[/math] is called bipartite if there is a partition of [math]\displaystyle{ V }[/math], [math]\displaystyle{ V=V_{1} \dot\cup V_{2} }[/math], such that for every edge [math]\displaystyle{ \{ v,w \} \in E }[/math] it is [math]\displaystyle{ v \in V_{1} \Leftrightarrow w \in V_{2} }[/math].
Absence of odd cycles
Theorem: An undirected graph [math]\displaystyle{ G=(V,E) }[/math] is bipartite if, and only if, [math]\displaystyle{ G }[/math] has no cycle of odd length.
Proof:
- First suppose [math]\displaystyle{ G }[/math] contains at least one cycle [math]\displaystyle{ v_{1} - v_{2} - ... - v_{k} - v_{1} }[/math] of odd length [math]\displaystyle{ k \in \N }[/math]. Without loss of generality, we assume [math]\displaystyle{ v_{1} \in V_{1} }[/math]. Then it is [math]\displaystyle{ v_{i} \in V_{1} }[/math] for all odd [math]\displaystyle{ i }[/math] and [math]\displaystyle{ v_{i} \in V_{2} }[/math] for all even [math]\displaystyle{ i }[/math]. The edge [math]\displaystyle{ \{ v,w \} }[/math] contradicts bipartiteness.
- Now suppose that [math]\displaystyle{ G }[/math] contains no cycle of odd length. We will prove bipartiteness constructively. Without loss of generality, we may assume that [math]\displaystyle{ G }[/math] is connected (otherwise, each connected component may be considered separately). We choose an node [math]\displaystyle{ v\in V }[/math], which will be fix, and start with an arbitrary node [math]\displaystyle{ u \in V }[/math] and label each node "[math]\displaystyle{ x }[/math]" if its distance (smallest number of edges) from [math]\displaystyle{ v }[/math] is even, and "[math]\displaystyle{ y }[/math]" otherwise. Suppose for a contradiction that there is an edge [math]\displaystyle{ \{ v,w \} }[/math] such that both endnotes have the same label. Then the shortest paths from [math]\displaystyle{ u }[/math] to [math]\displaystyle{ v }[/math] and [math]\displaystyle{ w }[/math] plus this edge from an odd cycle (which is not simple but can be easily reduced to a simple cycle, which is odd again).