Kosaraju

General information

Algorithmic problem: Strongly connected components

Type of algorithm: loop

Abstract View

1. Apply a repeated depth-first search to [math]\displaystyle{ G }[/math], the output order is parenthetical.
2. Invert the output order of the nodes.
3. Let [math]\displaystyle{ G^t=(V,A^t) }[/math] be the transpose of [math]\displaystyle{ G=(V,A) }[/math].
4. Apply a repeated depth-first search to [math]\displaystyle{ G^t }[/math] with a modification: The order in which the nodes are considered as potential start nodes is the inverted parenthetical order from step 2.
5. The node sets from the individual applications of DFS inside step 4 are exactly the SCC of [math]\displaystyle{ G }[/math].

Correctness

First note that the transposition of all arcs does not change the SCC of a graph, so step 4 indeed processes the SCC of [math]\displaystyle{ G }[/math].

Construction of the condensed graph (example)

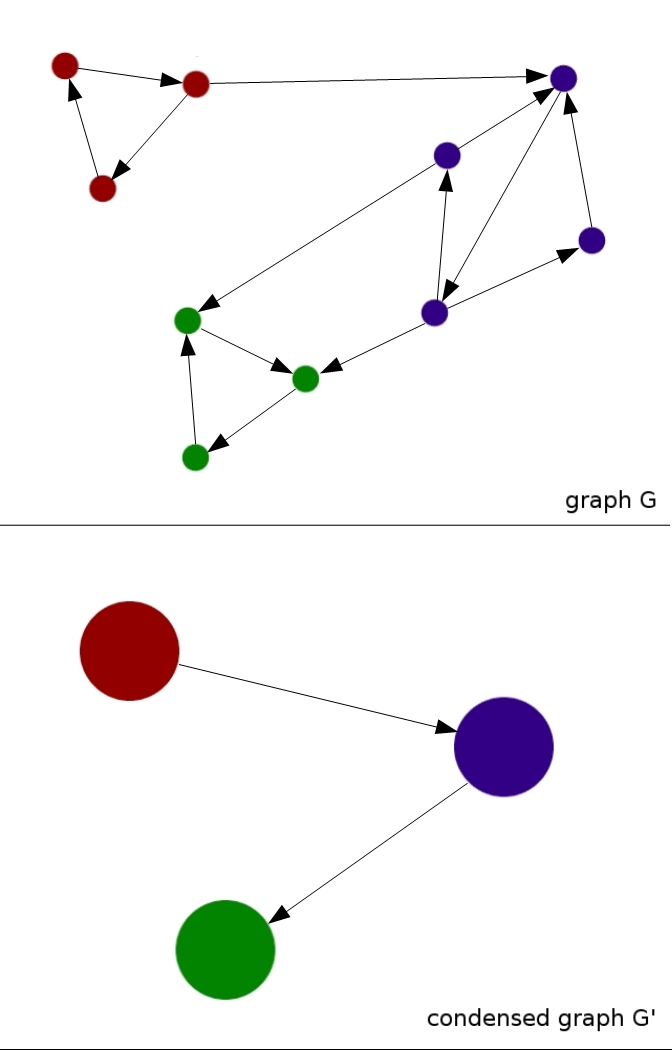
Consider the condensed graph [math]\displaystyle{ G' }[/math] whose nodes are these SCC, and there is an arc from an SCC [math]\displaystyle{ C_i }[/math] to an SCC [math]\displaystyle{ C_j }[/math] in [math]\displaystyle{ G' }[/math] if, and only if, there is at least one arc in [math]\displaystyle{ G }[/math] from some node in [math]\displaystyle{ C_i }[/math] to some node in [math]\displaystyle{ C_j }[/math]. This condensed graph is acyclic because all nodes in all SCC on a cycle would be mutually reachable from each other in [math]\displaystyle{ G }[/math] and their union would consequently form a single larger SCC contradicting the construction of the condensed graph.

In step 1, each DFS run either meets all nodes of an SCC of [math]\displaystyle{ G }[/math] or none of the nodes of this SCC. More specifically, all nodes in the same SCC as the start node and in all SCC reachable from that SCC, except for the SCC processed in previous DFS runs.

It is easy to see that all nodes of an SCC are finished consecutively (because of the parenthetical order); that is, all nodes of an SCC form a connected subsequence in the output sequence of step 1. In particular, it does not matter in step 4 which node of an SCC is chosen as a start node for a DFS run. If an SCC [math]\displaystyle{ C_i }[/math] is reachable from an SCC [math]\displaystyle{ C_j }[/math] in [math]\displaystyle{ G }[/math], then the nodes of [math]\displaystyle{ C_i }[/math] appear before the nodes of [math]\displaystyle{ C_j }[/math] in parenthetical order. Equivalently, the nodes of [math]\displaystyle{ C_i }[/math] appear after the nodes of [math]\displaystyle{ C_j }[/math] in the reverse order on which step 4 is based.

Let [math]\displaystyle{ C_i }[/math] and [math]\displaystyle{ C_j }[/math] be two SCC of [math]\displaystyle{ G }[/math]. Since each SCC is processed exhaustively or not at all in a DFS run, it suffices to show that [math]\displaystyle{ C_i }[/math] and [math]\displaystyle{ C_j }[/math] are not processed within the same run of step 4. Suppose for a contradiction that [math]\displaystyle{ C_i }[/math] and [math]\displaystyle{ C_j }[/math] are processed in the same DFS run in step 4 (not necessarily in the same run in step 1). Let [math]\displaystyle{ C_k }[/math] be the SCC to which the start node of that run belongs (possibly [math]\displaystyle{ k=i }[/math] or [math]\displaystyle{ k=j }[/math]). Without loss of generality, suppose [math]\displaystyle{ k\neq i }[/math]. Then [math]\displaystyle{ C_i }[/math] is reachable from [math]\displaystyle{ C_k }[/math] in [math]\displaystyle{ G' }[/math]; in other words, [math]\displaystyle{ C_k }[/math] is reachable from [math]\displaystyle{ C_i }[/math] in [math]\displaystyle{ G }[/math]. However, then the nodes of [math]\displaystyle{ C_i }[/math] have higher finishing times than the nodes of [math]\displaystyle{ C_k }[/math], so some node of [math]\displaystyle{ C_i }[/math] had been chosen as a start node before any node of [math]\displaystyle{ C_k }[/math].

Complexity

Statement: The asymptotic complexity is in [math]\displaystyle{ \Theta(|V|+|A|) }[/math].

Proof: Follows immediately from the linear asymptotic complexity of repeated DFS.

Pseudocode

STRONGLY-CONNECTED-COMPONENTS(D)
1 call DFS(D) to compute finishing times f[v] for each vertex v ∈ V
2 compute DT (w.r.t. step 3)
3 call DFS(DT), but in the main loop of DFS, consider the vertices in order of decreasing f[v] as computed in step 1
4 output the vertices of each tree in the DFS forest of step 3 as a separate strongly connected component